正八面體

頂點數目：6

邊數目：12

面數目：8

當邊長為a時：

表面積：

體積：

外接球半徑：(外接球即過正八面體各頂點的球)

內切球半徑： （內切球即與正八面體各面相切的球）

中交球半徑：（中交球即過正八面體各邊中點的球）

正八面體是五種正多面體的第三種，是三維的正軸體，有6個頂點、12條邊和8個面。它由八個等邊三角形構成，也可以看做上、下兩個正方椎體黏合而成，每個正方椎體由四個三角形與一個正方形組成。正八面體的對偶多面體是立方體。

正八面體內嵌在立方體中時，6個頂點分別位於立方體的面心：

正八面體體積 : 立方體體積

=1 : 6

以棱長為的正八面體的幾何中心作為原點，將正八面體的對角線作為x,y,z軸建立三維直角坐標系（正八面體的3條對角線兩兩正交，這也是正八面體被叫做“正軸形”的原因），則我們能將正八面體的頂點坐標記為

( ±1, 0, 0 )

( 0, ±1, 0 )

( 0, 0, ±1 )

正八面體表面方程為：

更一般的，如果正八面體的對角線平行於坐標軸，中心為()，外接圓半徑為r（棱長為），則正八面體表面方程為：

如果中心在原點的正八面體被拉長，成為菱形體，則更一般的八面體方程為

其內接於橢球體

表面積S和體積V為：

它的慣性張量I是：

當時，菱形體為上述正八面體。

正八面體可以以多種不同的方向被正交投影到二維平面，以下表格展示了幾種特殊的投影：

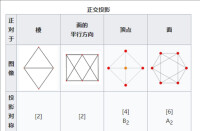
正八面體作為3維的正軸體正多面體，自身擁有較高的對稱性，它的所有面都是不可區分的。可是我們也可以想象將正八面體的面“塗上”不同的“顏色”，使它其的不同面擁有不同的“幾何意義”，使正八面體擁有不同的對稱性。正八面體的對稱群是（正八面體群），是三維的超正八面體群。在此對稱性下，正八面體的所有面都帶有相同對“顏色”，對稱性最高，群階48。該群的子群體現了正八面體更低的對稱性：（群階24），截半正四面體的對稱群；（群階12），三角反稜柱的對稱群；（群階16），四角雙稜錐（正四稜柱的對偶）的對稱群；（群階8），三維長菱體（三維長方體的對偶）的對稱群。

正八面體的對偶多面體是立方體。

當正八面體在立方體之內：

正八面體體積: 立方體體積

=[(1/3)×高×底面積]×2: 邊

=(1/3)(n/2)[(n)/2]2: n

=1: 6

柏拉圖認為正八面體介於正四面體（火）和正二十面體（水）之間，因此認為它代表的元素是空氣。