內點法
John von Neumann發明的演演算法
內點法 ()是一種求解線性規劃或非線性凸優化問題的演演算法。它是由John von Neumann發明的,他利用戈爾丹的線性齊次系統提出了這種新的求解線性規劃的方法。后被Narendra Karmarkar於1984年推廣應用到線性規劃,即Karmarkar演演算法。
1972年,V.Klee和G.Minty給出一個例子,他們構造一個線性規劃問題,用單純形方法求解,需要的計算時間為。這個例子表明,單純形演演算法雖然在實際應用中非常有效,至今佔有絕對優勢,但在理論上它還不是多項式演演算法。於是產生這樣的問題:對於線性規劃,能否找到多項式演演算法?
1979年,前蘇聯數學家第一個給出了求解線性規劃的多項式演演算法,這就是所謂的橢球演演算法。它的計算複雜性為,其中n是變數的維數,L是輸入長度。這個演演算法在理論上是重要的,但是計算結果很不理想,遠不及單純形方法有效。
演演算法上突破性的進展和當代科學技術發展的需要,又給人們提出進一步的問題:能否找到實用上也確實有效的多項式時間演演算法?正是在這樣的背景下,產生了內點法,它的計算複雜性是。
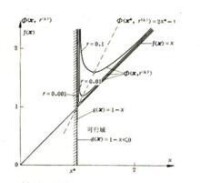
內點法中有一個懲罰函數,用於描述凸集。與單純形法不同,它通過遍歷內部可行區域來搜索最優解。
線性規劃問題描述如下:
與(1)對應的對數型懲罰函數為:
這裡是一個小的正參數,常被稱作“懲罰因子”。當趨近於0時,將趨近於(1)的解。
懲罰函數的梯度為:
是原始函數的梯度,且是的梯度。
(4)有時被稱為擾動互補條件,類似於KKT條件中的互補鬆弛。我們試圖找到那些使得懲罰函數梯度為0的。
對比(3)與(4)我們容易得到一個關於梯度的等式:
其中,是限制條件的雅克比矩陣。
(5)式意味著的梯度應該位於限制條件梯度所張成的子空間中。對(4)和(5)應用牛頓法我們得到:
其中,是的黑塞矩陣,是的的對角矩陣。
因為(1)和(4),所以在每次迭代時都必須滿足,所以可以通過選擇合適的來計算:
• 單純形法最古老,被研究的最為透徹,商業化的軟體程序也最成熟
• 橢球演演算法像曇花一現,雖然在理論上證明了線性規劃問題可在多項式時間內求解,但在實際應用上反而不如單純形法來的有效便捷
• 內點法是最新的設計,理論上它比橢球法還要有效,實際應用上它也可以與單純形法相抗衡,不少商業化軟體已經上市,前景甚佳