卡比博-小林-益川矩陣
卡比博-小林-益川矩陣
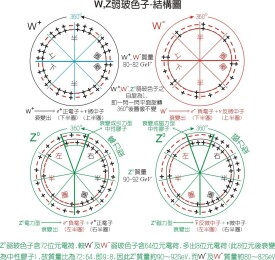
卡比博-小林-益川矩陣(Cabibbo-Kobayashi-Maskawa,CKM或KM matrix)是粒子物理標準模型的一個重要組成成份,它表徵了頂類型和底類型夸克間通過W粒子弱相互作用的耦合強度。
CKM矩陣也可用所謂的幺正三角形來圖像表示。最常見的是正交關係
1973年日本物理學家小林誠和益川敏英把它推廣到三代夸克。三代矩陣含有相位,可以用來解釋弱相互作用中的電荷宇稱對稱性破缺(CP破壞),也被經常用來解釋宇宙重子數不對稱。CKM矩陣在輕子中的對應是真木-中川-坂田矩陣(Maki-Nakagawa-Sakata或MNS)。
早期的粒子物理模型包涵三種夸克—上夸克、下夸克和奇異夸克。在研究強子的弱衰變中,人們發現奇異數守恆的過程要比不守恆的過程進行得快約20倍。為解釋此現象,卡比博引入了一個下夸克和奇異夸克(這兩種夸克有相同的量子數)之間的混合角θc。上夸克與下夸克和奇異夸克的相互作用耦合分別正比於此角的餘弦和正弦。實驗上sinθc約為0.23。
1973年,在一篇發表在日本期刊《理論物理學進展》上的題為“弱相互作用可重整化理論中的CP破壞”的論文中,小林誠和益川敏英把卡比博角推廣到三代夸克。他們發現雖然一般的三維幺正矩陣有九個實參數,但是只有四個具有物理意義,而其它的都可以被吸收到夸克波函數的位相中而不為觀測。四個物理參數中的一個是位相因子,它提供了CP破壞的微觀機制,同時猜測了第三代夸克的存在,因此具有重大的物理意義。他們二人也因而與南部陽一郎分享了2008年諾貝爾物理學獎。
如今,尋找CKM矩陣參數的微觀物理起源是粒子物理理論研究的重大課題之一。
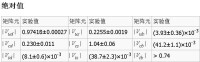
CKM矩陣是一個三維幺正矩陣。在標準參數化下,它可以由三個混合角和一個相位表示為(圖一)
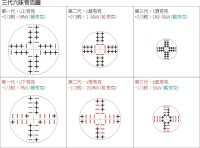
三代夸克圖
圖一
其中和分別代表三代頂類型(上、粲、頂)和底類型(下、奇異、底)夸克,c12,s12等是,等的簡寫。
實驗上CKM矩陣參數滿足,描寫這一重要特性的一個常用參數化表示是由美國物理學家沃爾芬斯坦(Wolfenstein)給出的。記(圖二)

圖二
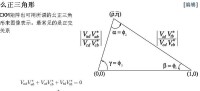
CKM矩陣也可用所謂的幺正三角形來圖像表示。最常見的是正交關係。
用測量最精確的項來歸一,此關係可以表示為複平面上的三角形,其三頂點坐標分別為(0,0),(1,0)和(,),如右圖所示。它的面積與位相參數表示化無關,是刻劃CP破壞的不變數。文獻中稱之為雅爾斯廓格(Jarlskog)不變數。
CKM矩陣的數學推導相當平庸。首先任意一個三維矩陣可以寫成歐拉形式,其中對角塊矩陣V1,V2,V3有以下形式(X代表非零元)(圖三)
其次注意到任意一個二維幺正矩陣可以表為(為幺模複數,)(圖六)
在上式中V2'仍是與V2同形的一般幺正矩陣,但可以繼續在V上左、右相乘與V2'和V3'對易的對角矩陣,即 diag型矩陣(α,β幺模),使得

圖六
(圖六)最後將所有的對角(相位)變換矩陣吸收到夸克波函數中去,V2',V1',V3'相乘即得CKM矩陣。
CKM矩陣元實驗測定和最新數據的詳細資料,可參閱粒子數據組的網頁和出版