增量

設f是從A到B的函數，A、B是某線性空間的子集，，對任意，稱為自變數在x₀處的增量，記為Δx，相應地，稱為f在x₀處的增量，記為Δf(x)或Δy(如果函數以表示)，增量這個詞可理解成增加的量，但可以取負值或0。

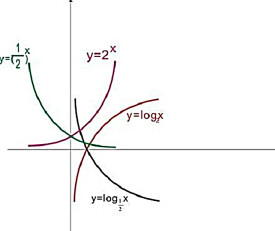
關於增量，不同的函數有不同的增長特點，自變數變化同樣的值對應的增量也是不同的，常見的幾類函數模型有

1．一次函數模型： (k，b為常數，)；

2．反比例函數模型： (k，b為常數，)；

3．二次函數模型： (a，b，c為常數，)；

4．指數型函數模型： (a，b，c為常數，；

5．對數型函數模型： (m，n，a為常數，)；

6．冪函數模型： (a，b，n為常數，)。

在區間上，儘管函數，和 都是增函數，但它們的增長速度不同，而且不在同一個“檔次”上。隨著x的增大，的增長速度越來越快，會超過並遠遠大於 的增長速度，而 的增長速度則會越來越慢。因此，總會存在一個，當 時，就有。