MSD
均方位移的縮寫
MSD是Mean Square Displacement縮寫,指的是均方位移。其定義為液體和氣體分子不會待在一個固定位置,而是不停移動的。MSD 均方根位移的量與原子的擴散係數存在對應關係。。。
Mean Squared Displacement,即均方位移。其定義如下:
其中是對組內所有原子平均。
如果只計算一個原子,MSD公式可以簡化為:
這是一個基本事實,否則它們不會具有流體的性質。舉個很顯然的例子:把一滴墨水滴入一杯清水中,過一會兒,墨水的顏色會均勻地分佈開來。明顯地,墨水分子分散到了整杯水中。這個過程就叫做 擴散,它很自然地發生在平衡態的流體中。
稠密流體中單一分子的運動並非沿著一個簡單的路徑。在它的移動過程中,它不斷和其它分子發生碰撞並被推離原本的方向。如果進一步仔細觀察它的路徑,就會發現,這非常近似於數學上隨機漫步(random walk)。這種路徑由 愛因斯坦在對布朗運動的研究中進行了著名的分析,他發現:做隨機漫步的粒子的移動距離的平方的平均數與時間成正比。這個關係式可以表示為:
其中,是位移平方的平均,t是時間,D和C是常數。D是其中最重要的參數,又叫做擴散係數(diffusion coefficient)。
當體系是固態時,即體系的溫度處於熔點以下,均方根位移存在上限值;當體系處於液態時,均方根位移與時間呈線性關係,而且其斜率與與原子擴散係數存在下列關係:
在分子動力學中的典型結果如圖所示:
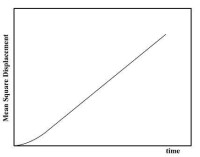
典型流體MSD曲線
