控制變數法

要了解控制變數法，首先要了解什麼是變數。

變數或變數，是指沒有固定的值，可以改變的數。變數以非數字的符號來表達，一般用拉丁字母。變數是常數的相反。變數的用處在於能一般化描述指令的方式。如果只能使用真實的值，指令只能應用於某些情況下。變數能夠作為某特定種類的值中任何一個的保留器。

變數用於開放句子，表示尚未清楚的值（即變數），或一個可代入的值（見函數）。這些變數通常用一個英文字母表示，若用了多於一個英文字母，很易令人混淆成兩個變數相乘。n,m,x,y,z是常見的變數名字，其中n,m較常表示整數。

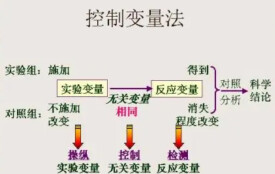
物理學中對於多因素（多變數）的問題，常常採用控制因素（變數）的方法，把多因素的問題變成多個單因素的問題。每一次只改變其中的某一個因素，而控制其餘幾個因素不變，從而研究被改變的這個因素對事物的影響，分別加以研究，最後再綜合解決，這種方法叫控制變數法。它是科學探究中的重要思想方法，廣泛地運用在各種科學探索和科學實驗研究之中。

1．獨立變數，即一個量改變不會引起除因變數以外的其他量的改變。只有將某物理量由獨立變數來表達，由它給出的函數關係才是正確的。

2．非獨立變數，一個量改變會引起除因變數以外的其他量改變。把非獨立變數看做是獨立變數，是確定物理量間關係的一大忌。

正確確定物理表達式中的物理量是常量還是變數，是獨立變數還是非獨立變數，不但是正確解答有關問題的前提和保障，而且還可以簡化解答過程。

方法點播：當一個問題與多個因素有關時，探究該問題與其中某個因素的關係時，通常採用控制變數法。

變數是統計學研究中對象的特徵。它可以是定性的也可以是定量的，一個定量變數要麼是離散的，要麼是連續的。社會科學中研究變數的關係，通常把一個變數稱為自變數（獨立變數），另一個變數稱之為因變數（依賴變數）

統計上的絕對量指標，按其取值的特點不同可分為離散變數與連續變數。

1．離散變數

離散變數亦可叫離散指標，是指僅能表現為整體取值的指標。

2．連續變數

連續變數亦可叫連續指標，是指可以出現小數的指標。

探究影響蒸發快慢的因素，探究聲音的響度和音調、理想斜面實驗、探究力與運動的關係、探究影響滑動摩擦力大小的因素、探究影響壓力的作用效果的因素、探究影響液體壓強大小的因素、探究影響浮力大小的因素、探究影響滑輪組的機械效率的因素、探究影響動能大小的因素、探究影響重力勢能大小的因素、驗證歐姆定律、探究電阻的電流與其兩端電壓的關係、探究影響電流做功多少的因素、探究影響電流的熱效應的因素、探究影響電磁鐵磁性強弱的因素。而且還需要試驗。

我們可以先將電壓人為的控制（即不變），改變電阻的大小，再測出各個電阻值所對應的電流的大小，從而可以得知電壓一定時，通過導體的電流和電阻成反比。控制變數法是為了研究物理量之間的關係。

s=vt即位移=速度*時間，這個公式可以用控制變數法來研究，就是說，知道“速度”、“位移”、“時間”，但為了研究出“位移=速度×時間”這個公式，我們要採用控制變數法。

研究的方法是這樣的：我們讓一輛小車勻速行駛一段時間，然後看它的位移。為了研究位移跟“速度”、“時間”是什麼關係，我們先讓小車以不同的屮相同的時間，比較兩種情況下行駛的位移。

例如：先以3m/s的速度行駛5秒，記下位移15m；接著以9m/s的速度行駛5秒，記下位移45m，這樣，我們可以看到在同樣的時間裡，速度增長了幾倍，位移也增長了幾倍，即位移和速度成正比。注意在這個例子中，我們故意讓小車兩次行駛的時間保持一致（都是5秒），從而就可以發現“位移和速度成正比”這個關係，因為是控制住“時間”這個變數，使其不變，來研究問題，所以這種方法叫“控制變數法”。同樣的，如果我們控制住“速度”這個變數，也同樣可以發現“位移和時間成正比”這個關係。（做法就是，讓小車以相同的速度行駛不同的時間，比較兩種情況下行駛的位移）也可以利用DIS實驗系統進行實驗（一般高中會有）。