全息術
全息術
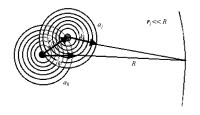
全息術,(holography)是利用干涉和衍射原理記錄並再現物體光波波前的一種技術。其第一步是利用干涉原理記錄物體光波信息,此即拍攝過程:被攝物體在激光輻照下形成漫射式的物光束(圖a);另一部分激光作為參考光束射到全息底片上,和物光束疊加產生干涉,把物體光波上各點的位相和振幅轉換成在空間上變化的強度,從而利用干涉條紋間的反差和間隔將物體光波的全部信息記錄下來。
全息術
全息照片可分為振幅型(又叫吸收型)和位相型兩大類,它們按照與被記錄時的曝光量相對應的方式分別改變照明光波的振幅或位相。如果根據干涉條紋的間距和感光膜層厚度的相對大小來劃分,則有薄型(二維型或平面型)和厚型(三維型或體積型)兩類全息照片。在厚型全息照片中,按拍攝時物光束與參考光束是否在感光膜的同側入射,分為透射型全息照片和反射型全息照片。如按記錄全息圖時光路布局的不同分類,有同軸型全息圖和離軸型全息圖。
全息術
又稱全息照相術。記錄波動干擾的振幅和位相分佈以及隨後使之重現的技術。廣泛地用作三維光學的成像,也可用於聲波(見聲全息)和射頻波。“全息”是由希臘字"holos"變來的,意即完全的信息──不僅包括光的振幅信息還包括位相信息。
發展簡史1947年D.伽柏從事提高電子顯微鏡分辨本領的工作。受W.L.布喇格在X射線金屬學方面工作及F.澤爾尼克的關於引入相干背景來顯示位相的工作的啟發,伽柏提出了全息術的設想以提高電子顯微鏡的分辨本領。1948年他利用水銀燈首次獲得了全息圖及其再現象,從而創立了全息術,為此他在1971年獲得了諾貝爾物理學獎。
50年代G.L.羅傑斯等人的工作大大擴充了波陣面再現理論。但是由於“孿生像”問題和光源相干性的限制,1955年以後全息術進入低潮階段。激光的出現,為全息術的發展開闢了廣闊的前景,1961~1962年,E.N.利思等人對伽柏全息圖進行了改進,引入“斜參考光束法”一舉解決了“孿生像”問題,用氦氖激光器成功地拍攝了第一張實用的激光全息圖。這樣就使得全息術在1963年以後成為光學領域中最活躍的分支之一。1964年利思等人又提出了漫射全息圖的概念,並得到三維物體的再現。與此同時,蘇聯的物理學家根據李普曼彩色照相法和伽柏全息法提出了反射全息圖的概念。1965年以來全息術的一個重要分支──脈衝全息術得到了發展,這使得動態全息干涉計量獲得了實際應用。
全息術
波陣面記錄這個過程中,引入適當的相干參考波,使它與由物體衍射(或散射)的光(物光)相干涉,把這干涉場記錄下來,即可得到一張全息圖。全息圖是與物體毫不相似的干涉圖,它上面不僅記錄了物光的振幅信息而且也把在普通照相過程丟失的位相信息記錄下來。記錄如圖1a所示。設在記錄媒質如干板處物光和參考光波陣面的復振幅表達式分別由波的疊加原理知,照相干板記錄下的總的光強分佈是:
把照相干板(或其他記錄媒質)放在(x,y)面內曝光,經過顯影、定影后,就會把I(x,y)以復振幅透過率τ(x,y)的形式記錄下來。在一定的條件下τ(x,y)∝I(x,y),式中τo(x,y)只和參考光的光強有關;第二項與物光的光強(或振幅)有關;第三項由參考光和物光的位相來決定。這樣全息圖的復振幅透過率τ(x,y)就是對物光振幅和位相的完全記錄。
波陣面再現波陣面記錄的結果是得到一張記有物光振幅和位相信息的全息圖。波陣面再現過程是利用適當的相干再現光B(x,y)照射全息圖而得到物的實像或虛像。用相干再現光B(x,y)照射全息圖,則透過全息圖的光μ(x,y),
通常再現光B(x,y)選為A(x,y)或A*(x,y),當B(x,y)=A(x,y)時,如果經適當選擇使|A(x,y)|2在各處有均勻的分佈,則μ4就代表物光O(x,y)的再現,即得到物的三維虛像。當B(x,y)=A*(x,y)時,同樣適當選擇A(x,y)使|A(x,y)|2在各處有均勻分佈時,則μ3(x,y)就代表物光的共軛光,得到物的三維實像。而在這兩種情況中的其他各項以均勻背景或畸變像出現。在技術上可以想辦法把它們消除或減少它們的影響。
全息術
同軸全息圖和離軸全息圖
1948年,伽柏利用透明體的透射光為參考光,散射光為物光,記錄了第一張全息圖──同軸全息圖。由於這種全息圖再現時有孿生像問題,利思等人引入斜參考光束,就得到了離軸全息圖,克服了孿生像問題。
薄全息圖和厚全息圖
當全息圖所記錄下來的干涉條紋間距大於記錄媒質厚度時,它可以看作是二維光柵結構,稱之為薄全息圖或平面全息圖。否則,全息圖可以看作三維光柵結構,稱之為厚全息圖或體全息圖。實際上,一張全息圖通常包含著不同間隔的條紋結構,所以它可能同時表現出薄結構和厚結構兩種特性來。例如,對於柯達649F干板(厚度≈16微米、n≈1.5)來說,只有在物光、參考光夾角小於10度時,所製作的全息圖才是薄全息圖。
透射全息圖與反射全息圖
全息術
振幅型全息圖和位相型全息圖
根據全息圖的形成機理可以知道,它是以某種方式把物光和參考光干涉所形成的駐波場在全息圖面上的光強分佈I(x,y),轉化為全息干板(或其他記錄媒質)的復振幅透過率τ(x,y)。一般τ(x,y)可以用下式表示:(1)對於銀鹽照相干板一類的記錄媒質,處理后可使嗞(x,y)為常數,可令為0。則(2)具有式(2)這種由吸收大小決定振幅透過率分佈的全息圖,叫作振幅型全息圖。對於漂白銀鹽干板、重鉻酸明膠板、摻鐵鈮酸鋰等媒質來講,τ(x,y)≈1,則復振幅透過率為(3)這一類全息圖上只有位相嗞(x,y)受I(x,y)的調製,叫作位相型全息圖。位相型全息圖具有均勻的透過率,但由於厚度不同或折射率變化而引起入射光的位相變化。它的特點是衍射效率高。表1給出了各種全息圖的理論最大衍射效率η。
菲涅耳型和夫琅和費型全息圖
當二維物體距全息圖面為有限值時形成菲涅耳全息圖,再現時,衍射波復振幅為物波復振幅的菲涅耳變換。若物體為三維分佈時,則再現得到三維物體的像,像全息圖可以看作是菲涅耳全息圖的一種,它是由物體的像所形成的全息圖。在物體的大小比起它距全息圖面的距離小很多時,就得到夫琅和費全息圖。再現時衍射波復振幅為物波復振幅的傅里葉變換。在這種條件下形成的全息圖叫作夫琅和費全息圖。傅里葉全息圖是夫琅和費全息圖的一種,它是利用透鏡把二維物體成像於無限遠處(把物放於透鏡的焦平面上),並使用相干的平面波作參考波,這相當於無限遠的像與參考波干涉,就得到了傅里葉全息圖。此外還有無透鏡傅里葉全息圖。
全息術
它的優點很多,如計算機可與灰階繪圖儀一起使用,特別是在計算全息中常常使用黑白全息圖或稱為二進位全息圖,可使記錄媒質的非線性影響降低到相當小程度;另外由於計算機和繪圖儀的可靠性,使得計算全息圖的重複質量得到了保證;此外對於光學上難以得到的複雜物體,利用計算機可根據其數學表達式作出全息圖並得到再現像,從而可以把計算機當作廣義的光學元件來使用。因此計算全息一出現就受到普遍重視,在諸如光學空間濾波、檢驗光學表面、三維計算機顯示等方面都獲得越來越多的應用。
計算全息圖的製作主要包括兩個步驟:第一步是計算,利用設想物的數學模型計算出該物波與相干的參考波在全息圖面上疊加后的光強分佈。這一步也可以不用參考波,不用參考波計算出來的是物波的分佈。第二步是繪圖,把計算機算出的全息圖的復振幅透過率分佈用繪圖儀繪出,經光學微縮或直接由電子計算機控制電子束繪圖機進行繪製,就得到計算全息圖。
全息術
彩虹全息的衍射光有會聚性能,再現像的亮度較高。採用白光照明光源,可以避免相干散斑紋效應引起的雜訊影響。彩虹全息圖是在物體實像附近記錄的。根據產生實像的方法不同可分為一步法彩虹全息術和二步法彩虹全息術。二步法彩虹全息術的實像是由作為母片的一般全息圖產生的。
一步法彩虹全息術的實像是由成像透鏡產生的法彩虹全息術的記錄光路圖。物體通過狹縫經透鏡成像。參考光在狹縫的上方(或下方)斜射到干板上。再現時,白光點光源位於記錄時參考光源的位置。白光被色散從而將狹縫像成在不同的垂直位置。眼睛在不同高度就看到不同顏色的像。眼睛在水平觀察範圍內移動,可以看到再現像的立體效果。
伽柏發明全息術不久,就指出它的三個方面的應用前景即全息干涉量度術、全息光學元件和全息信息存儲。隨著激光器的問世,這三方面都獲得了不同程度的實用化。後來又擴展到全息立體顯示、全息變換、特徵識別等方面。全息術在科技、文化、工業、農業、醫藥、藝術、商業等領域都獲得了一定程度的應用。但是由於種種技術原因,最有效的應用仍是全息干涉量度術和全息光學元件。