邊界層
路德維希·普朗特提出的力學名詞
邊界層,又稱附面層是一個流體力學名詞,表示流體中緊接著管壁或其他固定表面的部份。邊界層是由黏滯力產生的效應,和雷諾數Re有關。一般提到的邊界層是指速度的邊界層。在邊界層外,流體的速度接近定值,不隨位置而變化。在邊界層內,在固定表面上流速為0,距固定表面越遠,速度會趨近一定值。
層概念.普朗海德堡舉行的第三屆國際數學家大會上提出的。他在《具有很小摩擦的流體流動》一文中指出:“沿固體壁面的流動,可分成兩個區域,在表面附近的薄層部分,流體中的內摩擦即粘性起重要作用;在該層以外的其餘部分,粘性可以忽略。”也就是說,在邊界層以內的流體是粘性流體,可用納維-斯托克斯方程(見運動方程)描述;在邊界層以外的流體,可視為理想流體,用歐拉方程描述。自此以後,在流體力學研究中長期存在的兩條基本途徑,即從經驗角度研究有粘性的實際流體和從理論角度研究無粘性理想流體,得到了統一。普朗特的這篇論文是創立邊界層理論的起點。邊界層理論是研究邊界層中粘性流體運動規律的理論,既適用於處理流體沿固體壁面的流動,也用於研究無壁面的自由湍流(如射流)。它是研究粘性流體流動的動量傳遞、熱量傳遞和質量傳遞的理論基礎。
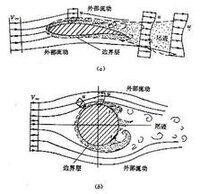
邊界層
層厚沿流流斷增,流,厚仍。限,層厚約。邊界層中的流體速度,在很短距離內從零急劇增長到相當於外流速度的數量級,速度梯度很大。因此,在邊界層內,粘性作用不能忽略,這是流體運動經受阻力的原因。
速度邊界層厚度
邊界層內從物面(當地速度為零)開始,沿法線方向至速度與當地自由流速度U 相等(嚴格地說是等於0.990或0.995U)的位置之間的距離,記為 δ 。
邊界層厚度與流動的雷諾數、自由流的狀態、物面粗糙度、物面形狀和延展範圍都有關係。由繞流物體頭部(前緣)起,邊界層厚度從零開始沿流動方向逐漸增厚。當空氣流的雷諾數為時,在距前緣1米處,平板上層流邊界層的厚度為3.5毫米。在平滑平扳上,層流邊界層的厚度
(,這裡v為流體運動粘性係數);寫成等式時的常數值隨所選取邊界層厚度處的速度百分比(如選)而異,一般為。平滑平板上湍流邊界層的厚度.
其比例常數約為0.37。可以看出,由於測定邊界層厚度有任意性,用它來計算摩擦阻力太粗糙,因而在實際應用中,又定義出其他的厚度。例如在低速時用位移厚度、動量(損失)厚度,此外還有一個無量綱厚度比叫形狀因子。
位移厚度
位移厚度的涵義是,邊界層內的流體受到阻滯,因而通過的流量減小,相當於理想繞流中外流從物面上向外推移了一個距離,繞流物體的形狀變成原幾何形狀再加位移厚度。
由於流體粘性阻滯而形成的邊界層把層外主流從壁面向外推移的距離(圖2),可按定義由下式求出:
平行流流過平板時,層流邊界層的,湍流邊界層的。
動量(損失)厚度
因粘性阻滯,在邊界層內所損失的動量,相當於按層外主流速度U計算時,這個動量所佔的厚度,即
平行流流過平板時,層流邊界層的,湍流邊界層的,故。
形狀因子
上面兩個厚度比所組成的無量綱參數稱為形狀因子,通常表為:(在低速時也寫為H)因,故。在層流邊界層中,H的值由駐點附近的2.0到分離點的3.5。在湍流邊界層中,它的值不定.大約為。
自從O.雷諾對圓管流動的實驗證明管內流動先是層流然後過渡到湍流后,他用一無量綱比值(即雷諾數)作為流動參數。對於每一種特定形狀都有一個臨界雷諾數,例如圓管流動的臨界雷諾數為2000,超過這個值,層流就過渡到湍流(見層流)。在邊界層內存在著類似的臨界雷諾數概念,不過邊界層的雷諾數通常寫作
臨界雷諾數Re,可以通過實驗得出。層流向湍流過渡除與雷諾數關係最大外,還受其他許多參量的影響,例如外流的湍流度,逆壓梯度、流體吹入、流過凹面上的離心力、非均勻流中的浮力、物面粗糙度、流體與物面的熱交換等,都會增加不穩定因素,容易引起層流邊界層的過渡。
層流邊界層穩定性理論
在理論方面,常用小擾動穩定理論,即假設層流流動是由平均流動(可看作定常流動)加上小擾動正弦流動合成的,如果小擾動隨時間的增加而增大,則是不穩定的,有可能過渡成湍流。通常所謂奧爾—索末菲方程就是小擾動理論的方程(見流體運動穩定性)。
討論平行流邊界層穩定性時,常用托爾明—施利希廷穩定性理論。它的基本思想是:層流邊界層流過物面時,總要受到一些小的擾動(如尖端、粗糙板面等),因而在層流邊界層中,包含有許多振幅非常小的速度脈動,其頻率範圍很廣。在某種情況下,若某一頻率的脈動得到加強,而其他頻率減弱.則前者在此頻率下迅速增大振幅(在邊界層內的這一波動叫作托爾明—施利希廷波),使層流不穩定,導致形成湍流。反之,如果脈動的所有頻率的振幅都減弱,則層流穩定。
層流邊界層向湍流邊界層的過渡
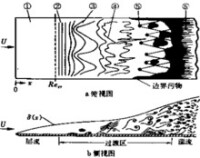
圖3 平板上層流邊界層過渡過程
渡是一個非常複雜的流動過程,直到目前為止.人們對它還沒有很清楚的了解。從繞平板這樣一個簡單流動來看,若外流湍流度低,流過平滑平板時,層流邊界層向湍流邊界層過渡大致經過以下幾個階段(圖3):
①靠近平板前端是穩定的層流邊界層,②過臨界雷諾數后.有不穩定的二維托爾明—施利希廷波;
③不穩定的層流三維波繼續發展,並形成小渦;
④在很強的局部剪應力處,渦旋破裂,產生三維湍流脈動;
⑤在湍流速度脈動很大的地方,產生許多湍流斑點;
⑥許多湍流斑點聯合在一起,發展成為完全發展了的湍流邊界層。
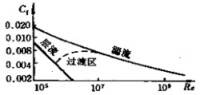
圖4 邊界層阻力係數Cf與雷諾數Re的關係
泡。在上述過程中,只能對①、②、③進行理論分析,其他各過程還有待於今後進一步探索,沿曲面有離心力的流動的不穩定性,與上述的不同。例如在兩個能作同心旋轉的內,外圓筒間的層流流動,當內筒旋轉外筒不動時產生泰勒渦(見流體運動穩定性),層流不穩定:而外筒旋轉內簡不動時,層流穩定;兩筒作相反方向旋轉時又不穩定。又如沿凹面的層流流動.產生垂直於流向的格特勒禍,也引起不穩定。
當層流邊界層過渡到湍流邊界后,邊界層厚度δ增大(圖3),同時阻力也增大。仍以平行流流過平板為例,阻力係數C與雷諾數Re兩者的關係如圖4(用雙對數坐標)所示。
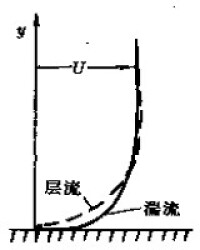
圖5 層流邊界層和湍流邊界層的比較
流邊界層。由於湍流是有渦流動,有隨機的脈動,流動隨空間和時間都在變化.所以湍流邊界層的內部結構比層流邊界層複雜得多。由於湍流內有垂直流向的動量交換,它在與壁面垂直截面上的速度分佈與層流邊界層的不同,下端豐滿一些(圖5)。
由實驗數據,可把湍流邊界層近似地看作由內區和外區組成。這樣的分法是因為靠近壁面的粘性剪應力與壓力梯度在這兩個區內是截然不同的。內區包括貼近壁面的粘性底層.其中剪應力最大,由許多小旋渦組成,向上是緩衝層,再向上直到邊界層外區是大尺寸旋渦組成的動量交換較大的湍流層.外區是從這個湍流層一直到速度與外流極相近的地方。總的說,內區占邊界層全層的。
湍流邊界層理淪
從湍流邊界層的研究歷史來看,存在著兩種理論,它們分別發展又相互關聯。一種是統計理論,另一種是半經驗理論。
①在統計理論中,把流體看做連續介質,把流速、壓力等的脈動值看做連續的隨機函數,通過各脈動值的相關函數和譜函數來描述湍流流動。按統計平均法,從中找出脈動結構,把各種平均值代入納維—斯托克斯方程及其他方程,得出所謂雷諾方程。但統計理論主要用於研究均勻各向同性湍流,對湍流邊界層流動並不適合。
②在另一種半經驗理論中因為湍流邊界層方程的數目少於未知量的數。方程組是不封閉的,因而需要補充一些關係式。由此而產生的一些不嚴謹的近似理論為半經驗理論。這些理論常無嚴格的依據,但對解決工程上的許多問題很有用處。又因為其中有些係數是從實驗中求出的,所以用這些半經驗理論算出的結果,常與實驗較吻合,但它們的適用範圍有局阻性。常用的半經驗理論有:J.V.布森涅斯克於1877年提出的,用渦粘性係數計算雷諾應力的公式,昔朗特的混合長理論(動量傳遞理論):G.I.泰勒的渦旋傳遞理論,卡門的相似理論等。這些半經驗理論的缺點是對湍流的內部結構都沒有做分析,使用範圍有限。
湍流邊界層實驗
對邊界層的研究,實驗是很重要的手段,尤其是湍流邊界層測量,許多國家都成立了小組在不斷地進行研究。一般實驗是在水槽或風洞內進行的。所用的流場顯示法有氫氣泡法,煙跡法,塗在物面上的袖流法等。測量方法近代多用熱線,熱膜和激光測速、激光全息攝影等(見湍流實驗)。

圖 6 繞翼剖面邊界層的分離
增加。由於在邊界層內的流體微團有動量損失,如遇到下游壓力增加(即有逆壓梯度)時,則動量再減少,直到流體微團不能再在物面上前進時就會從物面分離.這一現象叫做邊界層分離(圖76)。氣流開始離開物面的點稱為分離點.它的位置是由物面處的
來確定的,即該點在物面處的法向速度梯度為零.圖7表示出平行流流過對稱翼剖面的二維流動,在翼剖面後部有逆壓梯度處邊界層分離的情況,以及在分離點s附近的速度分佈。注意在分離點處的速度分佈曲線上有拐點,分離區內沿物面有反向(向前)的流動,產生渦旋,並形成物體後面的尾渦。機翼上邊界層分離,使機翼的舉力受到限制。並增加阻力。大攻角翼上分離會造成飛機的失逮,渦輪泵,壓氣機、螺旋槳等的漿葉上的氣流分離使機械效率降低,並能腐蝕壁面。
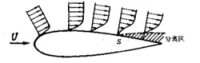
圖 7 平行流流過對稱翼剖面的二維流動
下游形成較大的旋渦區;這種分離在一般攻角時,常發生在機翼(舉例說)的後部(圖6和圖7);另一種是從分離點S,后,主流先離開物面,然後又在A點附著在物面上,形成氣泡——局部迴流區(圖8)。分離氣泡多是先層流分離,中間變為湍流,底層得到動能,再附著物面。在厚機翼時,分離常發生於機翼後部;在薄機翼時,則常在前緣附近產生氣泡分離。三維邊界層分離較複雜,甚至如何定義分離點,尚沒有一致的看法.湍流邊界層分離與層流邊界層分離相同,但因湍流內部有上下的動量交換,對同一外形物體,湍流邊界層的分離點比層流邊界層靠後。在特定情況下,人們可以人為地固定分離點,利用氣流分離后形成的渦旋對物體的作用,產生有利的效果,例如航空上採用邊條小翼,就是利用它的前緣分離渦,以增加小展弦比的基本翼上的非線性舉力。
在實驗方面,測分離點位置可用模型表面的油流法、絲線法和用普雷斯頓管等。
各國對分離流尤其是對二維非定常流和三維定常流中邊界層分離的起始及分離點,線附近流動問題的研究愈益重視,已有一些近似理論如三層結構等,也試提出二維、三維流動的分離判據,研究正在不斷深入中。
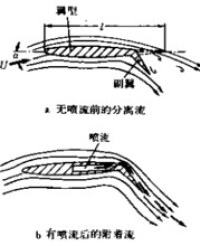
圖9
阻力增加和(或)舉力減少(甚至失速),因此人們很早就設法使機翼表面光滑,並設計“層流翼剖面”,以維持層流邊界層。但這種控制是有限的,所以人們後來採用了許多人工控制邊界層的方法,以達到影響邊界層結構,從而避免邊界層內氣流分離,和減少阻力增加舉力的目的。實驗和理論得出如下的使流體局部加速的幾種有效方法:①使部分物面移動,②通過物面上的噴孔(狹縫)吹出流體,以增加表面滯流的能量(圖9);③通過物面上的狹縫,吸走滯流,使邊界層變薄,以抑制分離;④用不同氣體噴射,加速滯流;⑤變更機翼形狀。
