映射

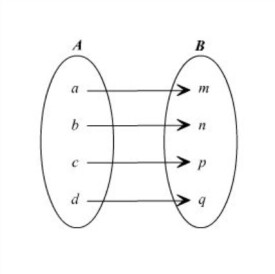
兩個非空集合A與B間存在著對應關係f，而且對於A中的每一個元素x，B中總有有唯一的一個元素y與它對應，就這種對應為從A到B的映射，記作f：A→B。其中，b稱為元素a在映射f下的象，記作：b=f(a)。a稱為b關於映射f的原象。集合A中所有元素的象的集合稱為映射f的值域，記作f(A)。

或者說，設A，B是兩個非空的集合，如果按某一個確定的對應關係f，使對於集合A中的任意一個元素x，在集合B中都有唯一的元素y與之對應，那麼就稱對應f：A→B為從集合A到集合B的一個映射。

映射，或者射影，在數學及相關的領域還用於定義函數。函數是從非空數集到非空數集的映射，而且只能是一對一映射或多對一映射。

映射在不同的領域有很多的名稱，它們的本質是相同的。如函數，運算元等等。這裡要說明，函數是兩個數集之間的映射，其他的映射並非函數。一一映射(雙射)是映射中特殊的一種，即兩集合元素間的唯一對應，通俗來講就是一個對一個（一對一）。

注意：(1)對於A中不同的元素，在B中不一定有不同的象；（2）B中每個元素都有原象（即滿射），且集合A中不同的元素在集合B中都有不同的象（即單射），則稱映射f建立了集合A和集合B之間的一個一一對應關係，也稱f是A到B上的一一映射。

映射的成立條件簡單的表述就是：

1．定義域又稱原像集，遍歷性：X中的每個元素x在映射的值域中都有對應對象

2．對應的唯一性：定義域中的一個元素只能與映射值域中的一個元素對應。值域又稱像集。

集合AB的元素個數為m，n，

那麼，從集合A到集合B的映射的個數為。

函數和映射，滿映射和單映射的區別。

函數是數集到數集映射，並且這個映射是“滿”的。

即滿映射f: A→B是一個函數，其中原像集A稱做函數的定義域，像集B稱做函數的值域。

“數集”就是數字的集合，可以是整數、有理數、實數、複數或是它們的一部分等等。

“映射”是比函數更廣泛一些的數學概念，它就是一個集合到另一個集合的一種確定的對應關係。即，若f是集合A到集合B的一個映射，那麼對A中的任何一個元素a，集合B中都存在唯一的元素b與a對應。稱a是原像，b是像。寫作f: A→B，元素關係就是b = f(a)。

一個映射f: A→B稱作“滿”的，就是說對B中所有的元素，都存在A中的原象。

在函數的定義中不要求是滿射，就是說值域應該是B的子集。（這個定義來源於一般中學中的講法，實際上許多數學書上並不一定定義函數是滿射。）

象集中每個元素都有原象的映射稱為滿射：即B中的任意一元素y都是A中的像，則稱f為A到B上的滿射，強調f(A)=B（B的原象可以多個）

原象集中不同元素的象不同的映射稱為單射：若A中任意兩個不同元素x1≠x2，它們的像f(x1)≠f(x2)，則稱f為A到B的單射，強調f(A)是B的子集。

單射和滿射可共同決定為一一雙射。

映射的不同分類是根據映射的結果進行的，從下面的三個角度進行：

1．根據結果的幾何性質分類：滿射（到上）與非滿射（內的）。

2．根據結果的分析性質分類：單射（一一的）與非單射。

3．同時考慮幾何與分析性質：滿的單射（一一對應）。

在很多特定的數學領域中，這個術語用來描述具有與該領域相關聯的特定性質的函數，例如，在拓撲學中的連續函數，線性代數中的線性變換等等。在形式邏輯中，這個術語有時用來表示函數謂詞（Functional predicate），在那裡函數是集合論中謂詞的模型。

如果將函數定義中兩個集合從非空集合擴展到任意元素的集合（不限於數），可以得到映射的概念：映射是數學中描述了兩個集合元素之間一種特殊的對應關係的一個術語。

按照映射的定義，下面的對應都是映射。

（1）設A={1，2，3，4}，B={3，5，7，9}，集合A中的元素x按照對應關係“乘2加1”和集合B中的元素對應，這個對應是集合A到集合B的映射。

（2）設A=N*，B={0，1}，集合A中的元素按照對應關係“x除以2得的餘數”和集合B中的元素對應，這個對應是集合A到集合B的映射。

（3）設A={x|x是三角形}，B={y|y>0}，集合A中的元素x按照對應關係“計算面積”和集合B中的元素對應，這個對應是集合A到集合B的映射。

（4）設A=R，B={直線上的點}，按照建立數軸的方法，是A中的數x與B中的點P對應，這個對應是集合A到集合B的映射。

（5）設A={P|P是直角坐標系中的點}，B={(x，y)|x∈R，y∈R}，按照建立平面直角坐標系的方法，是A中的點P與B中的有序實數對(x，y)對應，這個對應是集合A到集合B的映射。

“映射”或者“投影”，需要預先定義投影法則部分的函數後進行運算。因此“映射”計算可以實現跨維度對應。相應的微積分屬於純數字計算無法實現跨維度對應，運用微分模擬可以實現本維度內的複雜模擬。映射可以對非相關的多個集合進行對應的近似運算，而微積分只能在一個連續相關的大集合內進行精確運算。