橢圓
圓錐曲線的一種
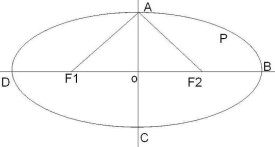
橢圓(Ellipse)是平面內到定點F1、F2的距離之和等於常數(大於|F1F2|)的動點P的軌跡,F1、F2稱為橢圓的兩個焦點。其數學表達式為:|PF1|+|PF2|=2a(2a>|F1F2|)。
徠橢圓是圓錐曲線的一種,即圓錐與平面的截線。
橢圓的周長等於特定的正弦曲線在一個周期內的長度。
在數學中,橢圓是圍繞兩個焦點的平面中的曲線,使得對於曲線上的每個點,到兩個焦點的距離之和是恆定的。因此,它是圓的概括,其是具有兩個焦點在相同位置處的特殊類型的橢圓。橢圓的形狀(如何“伸長”)由其偏心度表示,對於橢圓可以是從0(圓的極限情況)到任意接近但小於1的任何數字。
橢圓是封閉式圓錐截面:由錐體與平面相交的平面曲線(見右圖)。橢圓與其他兩種形式的圓錐截面有很多相似之處:拋物面和雙曲線,兩者都是開放的和無界的。圓柱體的橫截面為橢圓形,除非該截面平行於圓柱體的軸線。
橢圓也可以被定義為一組點,使得曲線上的每個點的距離與給定點(稱為焦點或焦點)的距離與曲線上的相同點的距離的比值給定行(稱為directrix)是一個常數。該比率稱為橢圓的偏心率。
也可以這樣定義橢圓,橢圓是點的集合,點其到兩個焦點的距離的和是固定數。
橢圓在物理,天文和工程方面很常見。例如,我們的太陽系中的每個行星的軌道大約是一個橢圓,其中一個焦點上的行星 - 太陽對的重心。衛星軌道行星和所有其他具有兩個天文體的系統也是如此。行星和星星的形狀通常被橢球描述。橢圓也出現在平行投影下的圓形圖像和透視投影的有界殼體,這是投影錐體與投影平面的簡單交點。當水平和垂直運動是具有相同頻率的正弦波時,它也是形成最簡單的李薩如圖。類似的效果導致光學中的光的橢圓偏振。
名叫ἔλλειψις(élleipsis,“遺漏”)由佩爾加的Apollonius在他的Conics中給出,強調了曲線與“應用領域”的聯繫。
阿波羅尼奧斯所著的八冊《圓錐曲線論(Conics)》中首次提出了今日大家熟知的 ellipse(橢圓)、parabola(拋物線)、hyperbola(雙曲線)等與圓錐截線有關的名詞,可以說是古希臘幾何學的精擘之作。直到十六、十七世紀之交,開普勒(Kepler)行星運行三定律的發現才知道行星繞太陽運行的軌道,是一種以太陽為其一焦點的橢圓。
平面內與兩定點、的距離的和等於常數( )的動點P的軌跡叫做橢圓。
即:
其中兩定點、叫做橢圓的焦點,兩焦點的距離 叫做橢圓的焦距。為橢圓的動點。
橢圓截與兩焦點連線重合的直線所得的弦為長軸,長為
橢圓截垂直平分兩焦點連線的直線所得弦為短軸,長為
可變為
橢圓平面內到定點(c,0)的距離和到定直線: (不在 上)的距離之比為常數(即離心率,0
其中定點 為橢圓的焦點,定直線 稱為橢圓的準線(該定直線的方程是(焦點在x軸上),或(焦點在y軸上))。
根據橢圓的一條重要性質:橢圓上的點與橢圓長軸(事實上只要是直徑都可以)兩端點連線的斜率之積是定值,定值為(前提是長軸平行於x軸。若長軸平行於y軸,比如焦點在y軸上的橢圓,可以得到斜率之積為 -a²/b²=1/(e²-1)),可以得出:
在坐標軸內,動點( )到兩定點( )( )的斜率乘積等於常數m(-1
注意:考慮到斜率不存在時不滿足乘積為常數,所以 無法取到,即該定義僅為去掉四個點的橢圓。
橢圓也可看做圓按一定方向作壓縮或拉伸一定比例所得圖形。
中心點為(h,k),主軸平行於x軸時,
高中課本在平面直角坐標系中,用方程描述了橢圓,橢圓的標準方程中的“標準”指的是中心在原點,對稱軸為坐標軸。
橢圓的標準方程有兩種,取決於焦點所在的坐標軸:
1)焦點在X軸時,標準方程為:
2)焦點在Y軸時,標準方程為:
橢圓上任意一點到F1,F2距離的和為2a,F1,F2之間的距離為2c。而公式中的b²=a²-c²。b是為了書寫方便設定的參數。
又及:如果中心在原點,但焦點的位置不明確在X軸或Y軸時,方程可設為mx²+ny²=1(m>0,n>0,m≠n)。即標準方程的統一形式。
橢圓的面積是πab。橢圓可以看作圓在某方向上的拉伸,它的參數方程是:x=acosθ , y=bsinθ
標準形式的橢圓在(x0,y0)點的切線就是:xx0/a²+yy0/b²=1。橢圓切線的斜率是:-b²x0/a²y0,這個可以通過複雜的代數計算得到。
x=acosθ , y=bsinθ。
求解橢圓上點到定點或到定直線距離的最值時,用參數坐標可將問題轉化為三角函數問題求解
x=a×cosβ, y=b×sinβ a為長軸長的一半 b為短軸長的一半
(一個焦點在極坐標系原點,另一個在θ=0的正方向上)
(e為橢圓的離心率=c/a)
1、範圍:焦點在 軸上, ;焦點在 軸上,
2、對稱性:關於X軸對稱,Y軸對稱,關於原點中心對稱。
3、頂點:(a,0)(-a,0)(0,b)(0,-b)
4、離心率: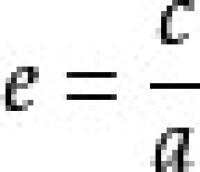 或 e=√(1-b^2/a²)
或 e=√(1-b^2/a²)
徠
5、離心率範圍:0可以證明以下命題:在橢圓焦點三角形中: ( 1)內點到一焦點的距離與以該焦點為端點的焦半徑之比為e(離心率)(2)內心將內點與非焦頂點連線段分成定必e (3)半焦距為內點,外點到橢圓中心距離的比例中項 證明:(1):在橢圓焦點三角形F1PF2中,設N為內點,由內角平分線性質和合比性質得: NF1 /PF1= NF2/PF2=(NF1+NF2 )/(PF1+PF2)=2C/2a=e (2) :設 內心為Q,則F1Q是∠F2F1P的內角平分線,則在△F1PN中,有QP/PF1=QN/NF1 ∴QN/QP=NF1/PF1 由(1)知NF1 /PF1=e 故QN/QP=e (3):設M是外點,由外角平分線和內角平分線性質:MF1/MF2=PF1/PF2=NF1/NF2 故(OM-c)/(OM+c)=(c-ON)/(c+ON) 故ON×OM=c²
6、離心率越小越接近於圓,越大則橢圓就越扁。
7、焦點(當中心為原點時):(-c,0),(c,0)或(0,c),(0,-c)
8、與(m為實數)為離心率相同的橢圓。
9、P為橢圓上的一點,a-c≤PF1(或PF2)≤a+c。
10.橢圓的周長等於特定的正弦曲線在一個周期內的長度。
定理1:設F1、F2為橢圓C的兩個焦點,P為C上任意一點。若直線AB切橢圓C於點P,且A和B在直線上位於P的兩側,則∠APF1=∠BPF2。(也就是說,橢圓在點P處的切線即為∠F1PF2的外角平分線所在的直線)
定理2:設F1、F2為橢圓C的兩個焦點,P為C上任意一點。若直線AB為C在P點的法線,則AB平分∠F1PF2。
上述兩定理的證明可以查看參考資料。
解析幾何法求證橢圓切線定理:
解:設C:((x^2)/(a^2))+((y^2)/(b^2))=1-----式1;
(a^2)-(b^2)=(c^2);
F1(-c,0);F2(c,0);P(xp,yp)
AB:(y-yp)=k(x-xp)=>y=kx+(yp-kxp);令m=yp-kxp=>AB:y=kx+m-----式2;
聯立式1和式2消去y得:((k^2)+((b^2)/(a^2)))(x^2)+2kmx+((m^2)-(b^2))=0;
因為直線AB切橢圓C於點P,所以上式只有唯一解,則:
4((km)^2)-4((k^2)+((b^2)/(a^2)))((m^2)-(b^2))=0=>m^2=((ak)^2)+(b^2);
m^2=(yp-kxp)^2=((yp)^2)+((kxp)^2)-2kxpyp=((ak)^2)+(b^2);
=>((a^2)-(xp^2))(k^2)+2xpypk+((b^2)-(yp^2));
由根的判別式得:4((xpyp)^2)-4((a^2)-(xp^2))((b^2)-(yp^2))=0;
所以k值有唯一解:k=(-2xpyp)/(2((a^2)-(xp^2)))=-xpyp/((a^2)-(xp^2));
由式1得:(a^2)-(xp^2)=(ayp/b)^2=>k=-(xp(b^2))/(yp(a^2));
m=yp-kxp=(((ypa)^2)+((xpb)^2))/(yp(a^2))=((ab)^2)/(yp(a^2))=(b^2)/yp;
設A0F1、B0F2分別過F1、F2垂直AB於A0、B0;
A0F1:(y-0)=(-1/k)(x+c)=>x+ky+c=0-----式3;
聯立式2和式3消去y得:x=-(km+c)/((k^2)+1);
聯立式2和式3消去x得:y= (m-kc)/((k^2)+1);
則:A0:(-(km+c)/((k^2)+1),(m-kc)/((k^2)+1));
|A0F1|^2=((m-kc)^2)/((k^2)+1));
同理:B0F2:(y-0)=(-1/k)(x-c);
=>B0:((c-km)/((k^2)+1),(m+kc)/((k^2)+1));
|B0F2|^2=((m+kc)^2)/((k^2)+1));
|PF1|^2=((xp+c)^2)+(yp^2);
|PF2|^2=((xp-c)^2)+(yp^2);
證明:若∠APF1=∠BPF2,則直角三角形A0PF1與直角三角形B0PF2相似;
=>|A0F1|/|PF1|=|B0F2|/|PF2|
=>(|A0F1|^2)/(|PF1|^2)=(|B0F2|^2)/(|PF2|^2)
=>(|PF2|^2)/(|PF1|^2)=(|B0F2|^2)/(|A0F1|^2)
((m+kc)^2)/((m-kc)^2)=(((xp-c)^2)+(yp^2))/(((xp+c)^2)+(yp^2));-----式4
m+kc=(b^2)/yp-(xpc(b^2))/(yp(a^2))=((a^2)-xpc)(b^2)/(yp(a^2));-----式5
m-kc=(b^2)/yp+(xpc(b^2))/(yp(a^2))=((a^2)+xpc)(b^2)/(yp(a^2));----式6
把式5和式6代入式4得:
(((a^2)-xpc)^2)/(((a^2)+xpc)^2)=(((xp-c)^2)+(yp^2))/(((xp+c)^2)+(yp^2));
=>(((a^2)-xpc)^2)(((xp+c)^2)+(yp^2))=(((a^2)+xpc)^2)(((xp-c)^2)+(yp^2))
=>(((a^2)-xpc)^2)((xp+c)^2)+(((a^2)-xpc)^2)(yp^2)=(((a^2)+xpc)^2)((xp-c)^2)+(((a^2)+xpc)^2)(yp^2)
=>[(((a^2)-xpc)^2)((xp+c)^2)-(((a^2)+xpc)^2)((xp-c)^2)]=[(((a^2)+xpc)^2)-(((a^2)-xpc)^2)](yp^2)
=>[((a^2)-xpc)(xp+c)+((a^2)+xpc)(xp-c)][((a^2)-xpc)(xp+c)-((a^2)+xpc)(xp-c)]=4xpc(ayp)^2
=>(2(a^2)xp-2(c^2)xp)(2c(a^2)-2c(xp^2))=4xpc(ayp)^2
=>4xpc(b^2)((a^2)-(xp^2))=4xpc(ayp)^2
=>(b^2)((a^2)-(xp^2))=(ayp)^2
=>(ab)^2=((ayp)^2)+((bxp)^2)
=>((xp^2)/(a^2))+((yp^2)/(b^2))=1等式成立,∠APF1=∠BPF2得證
設F1、F2為橢圓C的兩個焦點,P為C上任意一點,則在橢圓焦點三角形F1PF2中,分別稱∠F1PF2的內角平分線,外角平分線與橢圓長軸的交點為內點,外點。(如右圖中的N,M點為內點,外點)
橢圓的面鏡(以橢圓的長軸為軸,把橢圓轉動180度形成的立體圖形,其內表面全部做成反射面,中空)可以將某個焦點發出的光線全部反射到另一個焦點處;橢圓的透鏡(某些截面為橢圓)有匯聚光線的作用(也叫凸透鏡),老花眼鏡、放大鏡和遠視眼鏡都是這種鏡片(這些光學性質可以通過反證法證明)。
(其中 分別是橢圓的長半軸、短半軸的長),或(其中 分別是橢圓的長軸,短軸的長)。
證:的面積,由於圖形的對稱性可知,只要求出第一象限的面積乘以4即可。
在第一象限 , 令
橢圓周長計算公式:L=T(r+R)
T為橢圓係數,可以由r/R的值,查表找出係數T值;r為橢圓短半徑;R為橢圓長半徑。
橢圓周長定理:橢圓的周長等於該橢圓短半徑與長半徑之和與該橢圓係數的積(包括正圓)。
附橢圓係數簡表:
| 橢圓係數簡表 | |||||||
| r / R | 係數 | r / R | 係數 | r / R | 係數 | r / R | 係數 |
| 0.01 | 3.961483495 | 0.26 | 3.418920439 | 0.51 | 3.224856225 | 0.76 | 3.156214217 |
| 0.02 | 3.925332509 | 0.27 | 3.40695685 | 0.52 | 3.220415735 | 0.77 | 3.154868403 |
| 0.03 | 3.891174223 | 0.28 | 3.395457698 | 0.53 | 3.216154903 | 0.78 | 3.153601776 |
| 0.04 | 3.858791647 | 0.29 | 3.384403803 | 0.54 | 3.212067616 | 0.79 | 3.152411903 |
| 0.05 | 3.828024399 | 0.3 | 3.373776976 | 0.55 | 3.208148 | 0.8 | 3.151296432 |
| 0.06 | 3.798743616 | 0.31 | 3.363559954 | 0.56 | 3.204390411 | 0.81 | 3.150253089 |
| 0.07 | 3.770841059 | 0.32 | 3.353736335 | 0.57 | 3.200789422 | 0.82 | 3.149279677 |
| 0.08 | 3.744223265 | 0.33 | 3.344290532 | 0.58 | 3.197339815 | 0.83 | 3.148374067 |
| 0.09 | 3.718808013 | 0.34 | 3.335207712 | 0.59 | 3.194036571 | 0.84 | 3.147534204 |
| 0.1 | 3.694521982 | 0.35 | 3.326473758 | 0.6 | 3.190874858 | 0.85 | 3.146758097 |
| 0.11 | 3.671299121 | 0.36 | 3.318075219 | 0.61 | 3.187850029 | 0.86 | 3.146043822 |
| 0.12 | 3.649079455 | 0.37 | 3.309999276 | 0.62 | 3.184957608 | 0.87 | 3.145389514 |
| 0.13 | 3.627808177 | 0.38 | 3.302233702 | 0.63 | 3.182193286 | 0.88 | 3.144793371 |
| 0.14 | 3.607434941 | 0.39 | 3.294766828 | 0.64 | 3.179552911 | 0.89 | 3.144253646 |
| 0.15 | 3.587913299 | 0.4 | 3.287587514 | 0.65 | 3.177032484 | 0.9 | 3.143768649 |
| 0.16 | 3.569200238 | 0.41 | 3.280685115 | 0.66 | 3.174628151 | 0.91 | 3.143336742 |
| 0.17 | 3.551255799 | 0.42 | 3.274049459 | 0.67 | 3.172336195 | 0.92 | 3.14295634 |
| 0.18 | 3.534042762 | 0.43 | 3.267670819 | 0.68 | 3.170153034 | 0.93 | 3.142625907 |
| 0.19 | 3.517526368 | 0.44 | 3.261539886 | 0.69 | 3.168075214 | 0.94 | 3.142343956 |
| 0.2 | 3.50167409 | 0.45 | 3.255647754 | 0.7 | 3.166099401 | 0.95 | 3.142109044 |
| 0.21 | 3.486455429 | 0.46 | 3.249985893 | 0.71 | 3.164222379 | 0.96 | 3.141919775 |
| 0.22 | 3.471841741 | 0.47 | 3.244546132 | 0.72 | 3.162441046 | 0.97 | 3.141774794 |
| 0.23 | 3.457806077 | 0.48 | 3.239320639 | 0.73 | 3.160752407 | 0.98 | 3.141672788 |
| 0.24 | 3.444323049 | 0.49 | 3.234301909 | 0.74 | 3.159153568 | 0.99 | 3.141612486 |
| 0.25 | 3.43136871 | 0.5 | 3.22948274 | 0.75 | 3.157641737 | 1 | π |
| 工程運用橢圓係數簡表 | |||||||
| r / R | 係數 | r / R | 係數 | r / R | 係數 | r / R | 係數 |
| 1 | π | 0.4787 | 3.24 | 0.2011 | 3.5 | 0.0739 | 3.76 |
| 0.9555 | 3.142 | 0.4599 | 3.25 | 0.1946 | 3.51 | 0.0703 | 3.77 |
| 0.9188 | 3.143 | 0.4422 | 3.26 | 0.1884 | 3.52 | 0.0666 | 3.78 |
| 0.8951 | 3.144 | 0.4263 | 3.27 | 0.1824 | 3.53 | 0.0631 | 3.79 |
| 0.8764 | 3.145 | 0.4111 | 3.28 | 0.1764 | 3.54 | 0.0595 | 3.8 |
| 0.8607 | 3.146 | 0.3966 | 3.29 | 0.1707 | 3.55 | 0.0561 | 3.81 |
| 0.8468 | 3.147 | 0.3829 | 3.3 | 0.1651 | 3.56 | 0.0526 | 3.82 |
| 0.8433 | 3.148 | 0.3699 | 3.31 | 0.1595 | 3.57 | 0.0493 | 3.83 |
| 0.8231 | 3.149 | 0.3577 | 3.32 | 0.1541 | 3.58 | 0.0461 | 3.84 |
| 0.8126 | 3.15 | 0.3459 | 3.33 | 0.1489 | 3.59 | 0.0428 | 3.85 |
| 0.7689 | 3.155 | 0.3414 | 3.34 | 0.1437 | 3.6 | 0.0396 | 3.86 |
| 0.7347 | 3.16 | 0.3239 | 3.35 | 0.1387 | 3.61 | 0.0364 | 3.87 |
| 0.7058 | 3.165 | 0.3136 | 3.36 | 0.1337 | 3.62 | 0.0333 | 3.88 |
| 0.6806 | 3.17 | 0.3036 | 3.37 | 0.1289 | 3.63 | 0.0303 | 3.89 |
| 0.6584 | 3.175 | 0.2941 | 3.38 | 0.1242 | 3.64 | 0.0273 | 3.9 |
| 0.6383 | 3.18 | 0.2848 | 3.39 | 0.1195 | 3.65 | 0.0244 | 3.91 |
| 0.6199 | 3.185 | 0.2759 | 3.4 | 0.1149 | 3.66 | 0.0215 | 3.92 |
| 0.6028 | 3.19 | 0.2674 | 3.41 | 0.1105 | 3.67 | 0.0186 | 3.93 |
| 0.5871 | 3.195 | 0.2591 | 3.42 | 0.1062 | 3.68 | 0.0158 | 3.94 |
| 0.5722 | 3.2 | 0.2511 | 3.43 | 0.1019 | 3.69 | 0.0131 | 3.95 |
| 0.5583 | 3.205 | 0.2432 | 3.44 | 0.0977 | 3.7 | 0.0103 | 3.96 |
| 0.5452 | 3.21 | 0.2357 | 3.45 | 0.0935 | 3.71 | 0.0077 | 3.97 |
| 0.5328 | 3.215 | 0.2284 | 3.46 | 0.0895 | 3.72 | 0.0051 | 3.98 |
| 0.5097 | 3.225 | 0.2212 | 3.47 | 0.0855 | 3.73 | 0.0025 | 3.99 |
| 0.4989 | 3.23 | 0.2143 | 3.48 | 0.0816 | 3.74 | 0.0012 | 3.995 |
| 0.4886 | 3.235 | 0.2076 | 3.49 | 0.0777 | 3.75 | 0.0002 | 3.999 |
關於橢圓的周長等於特定的正弦曲線在一個周期內的長度的證明:
半徑為r的圓柱上與一斜平面相交得到一橢圓,該斜平面與水平面的夾角為α,截取一個過橢圓短徑的圓。以該圓和橢圓的某一交點為起始轉過一個θ角。則橢圓上的點與圓上垂直對應的點的高度可以得到f(c)=r tanα sin(c/r)
r:圓柱半徑
α:橢圓所在面與水平面的角度
c:對應的弧長(從某一個交點起往某一個方向移動)
以上為證明簡要過程,則橢圓(x*cosα)^2+y^2=r^2的周長與f(c)=r tanα sin(c/r)的正弦曲線在一個周期內的長度是相等的,而一個周期T=2πr,正好為一個圓的周長。
這是我在工作的時候,偶爾發現的,沒有引用,也沒有搜索到相關的文獻,可能有前輩在我之前就發現了,若有不妥,請諒解。
橢圓離心率的定義為橢圓上焦距與長軸的比值,(範圍:0
e=c/a(02c。離心率越大,橢圓越扁平;離心率越小,橢圓越接近於圓形。
橢圓的焦准距:橢圓的焦點與其相應準線(如焦點(c,0)與準線x=±a^2/c) 的距離為a^2/c-c=b^2/c
離心率與 的關係:
焦點在x軸上:|PF1|=a+ex |PF2|=a-ex(F1,F2分別為左右焦點)
橢圓過右焦點的半徑r=a-ex
過左焦點的半徑r=a+ex
焦點在y軸上:|PF1|=a+ey |PF2|=a-ey(F2,F1分別為上下焦點)
橢圓的通徑:過焦點的垂直於x軸(或y軸)的直線與橢圓的兩交點A,B之間的距離,即|AB|=2*b^2/a
過橢圓上x²/a²+y²/b²=1上一點(x,y)的切線斜率為 -b²X/a²y
若有一三角形兩個頂點在橢圓的兩個焦點上,且第三個頂點在橢圓上
那麼若∠F1PF2=θ,則S=b²tan(θ/2)。
K=ab/[(b²-a²)(cosθ)+a²]
(焦點在x軸上)
(焦點在y軸上)
准圓為
從准圓上任一點向橢圓引兩條切線,這兩條切線垂直。
l=2b^2/a
圓錐曲線(除圓外)中,過焦點並垂直於軸的弦
橢圓中的通徑是通過焦點最短的弦
點M(x0,y0)橢圓 x^2/a^2+y^2/b^2=1
點在圓內:x0/a+y0/b<1
點在圓上:x0/a+y0/b=1
點在圓外:x0/a+y0/b>1
跟圓與直線的位置關係一樣的
相交 相離 相切
y=kx+m ①
x/a+y/b=1 ②
由①②可推出xa+(kx+m)/b=1
相切△=0
相離△<0無交點
相交△>0 可利用弦長公式:設A(x1,y1) B(x2,y2)
求中點坐標
根據韋達定理 x1+x2=-b/a,x1x2=c/a
代入直線方程可求出 (y1+y2)/2=可求出中點坐標。
|AB|=d = √(1+k)[(x1+x2)-4x1*x2] = √(1+1/k)[(y1+y2)-4y1y2]
例如:有一個圓柱,被截得到一個截面,下面證明它是一個橢圓(用上面的第一定義):
將兩個半徑與圓柱半徑相等的半球從圓柱兩端向中間擠壓,它們碰到截面的時候停止,那麼會得到兩個公共點,顯然他們是截面與球的切點。
設兩點為F1、F2
對於截面上任意一點P,過P做圓柱的母線Q1、Q2,與球、圓柱相切的大圓分別交於Q1、Q2
則PF1=PQ1、PF2=PQ2,所以PF1+PF2=Q1Q2
由定義1知:截面是一個橢圓,且以F1、F2為焦點
用同樣的方法,也可以證明圓錐的斜截面(不通過底面)為一個橢圓
例:已知橢圓C:x^2/a^2+y^2/b^2=1(a>b>0)的離心率為√6/3,短軸一個端點到右焦點的距離為√3.
1.求橢圓C的方程.
2.直線l:y=x+1與橢圓交於A,B兩點,P為橢圓上一點,求△PAB面積的最大值.
3.在⑵的基礎上求△AOB的面積.
一 分析短軸的端點到左右焦點的距離和為2a,端點到左右焦點的距離相等(橢圓的定義),可知a=√3,又c/a=√6/3,代入得c=√2,b=√(a^2-c^2)=1,方程是x^2/3+y^2/1=1,
二 要求面積,顯然以ab作為三角形的底邊,聯立x^2/3+y^2/1=1,y=x+1解得x1=0,y1=1,x2=-1.5,y2=-0.5.利用弦長公式有√(1+k^2))[x2-x1](中括弧表示絕對值)弦長=3√2/2,對於p點面積最大,它到弦的距離應最大,假設已經找到p到弦的距離最大,過p做弦的平行線,可以 發現這個平行線是橢圓的切線是才會最大,這個切線和弦平行故斜率和弦的斜率=,設y=x+m,利用判別式等於0,求得m=2,-2.結合圖形得m=-2.x=1.5,y=-0.5,p(1.5,-0.5),
三 直線方程x-y+1=0,利用點到直線的距離公式求得√2/2,面積1/2*√2/2*3√2/2=3/4,
畫長軸AB,短軸CD,AB和CD互垂平分於O點。⑵:連接AC。⑶:以O為圓心,OA為半徑作圓弧交OC延長線於E點。⑷:以C為圓心,CE為半徑作圓弧與AC交於F點。⑸:作AF的垂直平分線交CD延長線於G點,交AB於H點。⑹:截取H,G對於O點的對稱點H’,G’ ⑺:H,H’為長軸圓心,分別以HA、H‘B為半徑作圓;G,G’為短軸圓心,分別以GC、G‘D為半徑作圓。
用一根線或者細銅絲,鉛筆,2個圖釘或大頭針畫橢圓的方法:先畫好長短軸的十字線,在長軸上以圓點為中心先找2個大於短軸半徑的點,一個點先用圖釘或者大頭針栓好線固定住,另一個點的線先不要固定,用筆帶住線去找長短軸的4個頂點,此步驟需要多次定位,直到都正好能於頂點吻合后固定住這2個點,用筆帶住線,直接畫出橢圓:)使用細銅絲最好,因為線的彈性較大畫出來不一定準確!
橢圓的焦距│FF'│(Z)定義,為已知橢圓所構成的長軸X(ab)與短軸Y(cd)則以長軸一端A為圓心短軸Y為半徑畫弧,從長軸另一段點B引出與弧相切的線段則為該橢圓焦距,求證公式為2√{(Z/2)^2+(Y/2)^2}+Z=X+Z(平面內與兩定點F、F'的距離的和等於常數2a(2a>|FF'|)的動點P的軌跡叫做橢圓),可演變為z=√x^2-y^2(x>y>0)。Z兩端點F、F'為定點。取有韌性切伸縮係數越小越好的線,環繞線段AF'或者FB線段任意一組為長度,以該長度為固定三角形周長,以F、F' 為定點、取構成該三角形上的第三點為動點畫弧則構成該橢圓。
環線長。根據橢圓的圖形特徵,採用環線表示動點與焦點間的距離關係,形成統一的圓形環線作圖法。具體方法簡介:(1)作圖工具為筆、大頭針、直尺和環形線。(環形線製作:取一段長度(30—50cm)和粗細適中彈性小的軟線、一段8mm長細電線空塑料管,軟線從塑料管中相向竄過,塑料管將軟線夾緊,但用力可以抽動,形成能收縮和放長的環形線)。(2)在作圖平面上作出各種圓形的定點和動點。(3)將大頭針分別直立、固定在定點上;(4)將符合長度的環形線套在大頭針外,畫筆由內向外拉直環線,通過調整環線的長度使筆尖剛好落在動點上;(5)將畫筆移動一周,即可作出各種圓的圖形。
環線作圖方法的最大特點,就是把圓形的動點與焦點間的距離關係以環線的方式聯繫起來,而不受焦點數目的影響,環線內可以容納任意焦點數目,為探討3個及其3個以上焦點數目的多焦點圓提供有效方法。環線作圖方法,屬於連續移動作圖法,適合不同大小的圓、橢圓和卵圓等作圖。
若用該方法畫規定半長軸a和半短軸b的橢圓,則,環線長
Ellipse函數
函數功能
該函數用於畫一個橢圓,橢圓的中心是限定矩形的中心,使用當前畫筆畫橢圓,用當前的畫刷填充橢圓。
函數原型
BOOL Ellipse(HDC hdc,int nLeftRect,int nTopRect,nRightRect,int nBottomRect).
參數
hdc:設備環境句柄。
nLeftRect:指定限定橢圓左上角的X坐標。
nTopRect:指定限定橢圓左上角的Y坐標。
nRightRect:指定限定橢圓右下角的X坐標。
nBottomRect:指定限定橢圓右下角的Y坐標。
返回值
如果函數調用成功,返回值非零;如果函數調用失敗,返回值是0。
計算機圖形學約束
橢圓必須一條直徑與x軸平行,另一條直徑y軸平行。不滿足此條件的幾何學橢圓在計算機圖形學上視作一般封閉曲線。
目錄