氫原子

1913 年，尼爾斯·玻耳在做了一些簡化的假設后，計算出氫原子的光譜頻率。這些假想，玻爾模型的基石，並不是完全的正確，但是可以得到正確的能量答案。

1925/26 年，埃爾文·薛定諤應用他發明的薛定諤方程，以嚴謹的量子力學分析，清楚地解釋了玻爾答案正確的原因。氫原子的薛定諤方程的解答是一個解析解，也可以計算氫原子的能級與光譜譜線的頻率。薛定諤方程的解答比玻爾模型更為精確，能夠得到許多電子量子態的波函數（軌道），也能夠解釋化學鍵的各向異性。

氫原子是氫元素的原子。電中性的原子含有一個正價的質子與一個負價的電子，被庫侖定律束縛於原子核內。在大自然中，氫原子是丰度最高的同位素，稱為氫，氫-1，或氕。氫原子不含任何中子，別的氫同位素含有一個或多個中子。這條目主要描述氫-1 。

氫原子擁有一個質子和一個電子，是一個的簡單的二體系統。系統內的作用力只跟二體之間的距離有關，是反平方有心力，不需要將這反平方有心力二體系統再加理想化，簡單化。描述這系統的（非相對論性的）薛定諤方程有解析解，也就是說，解答能以有限數量的常見函數來表達。滿足這薛定諤方程的波函數可以完全地描述電子的量子行為。因此可以這樣說，在量子力學里，沒有比氫原子問題更簡單，更實用，而又有解析解的問題了。所推演出來的基本物理理論，又可以用簡單的實驗來核對。所以，氫原子問題是個很重要的問題。

另外，理論上薛定諤方程也可用於求解更複雜的原子與分子。但在大多數的案例中，皆無法獲得解析解，而必須藉用電腦(計算機)來進行計算與模擬，或者做一些簡化的假設，方能求得問題的解析解。

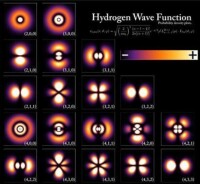
右圖顯示出能量最低的幾個氫原子軌道（能量本徵函數）。橫向展示不同的角量子數 (l) ,豎向展示不同的能級 (n)。

這些是概率密度的截面的繪圖。圖內各種顏色的亮度代表不同的概率密度（黑色：0 概率密度，白色：最高概率密度）。角量子數 l ，以通常的光譜學代碼規則，標記在每一個縱排的最上端。s 意指，p 意指 ，d意指 。主量子數 標記在每一個橫排的最右端。磁量子數m被設定為 0 。截面是 xz-平面（ z-軸是縱軸）。將繪圖繞著 z-軸旋轉，則可得到三維空間的概率密度。

基態是最低能級的量子態，也是電子最常找到的量子態，標記為1s態，, 。

特別注意，在每一個軌道的圖片內，黑線出現的次數。這些二維空間黑線，在三維空間里，是節面(nodal plane) 。節面的數量等於，是徑向節數與角節數的總和。

思考氫原子穩定性問題，應用經典電動力學來分析，則由於庫侖力作用，束縛電子會被原子核吸引，呈螺線運動掉入原子核，同時輻射出無窮大能量，因此原子不具有穩定性。但是，在大自然里這虛擬現象實際並不會發生。那麼，為什麼氫原子的束縛電子不會掉入原子核里？應用量子力學，可以計算出氫原子系統的基態能量大於某有限值，稱這結果為滿足“第一種穩定性條件”，即氫原子的基態能量大於某有限值：

量子力學的海森堡不確定性原理可以用來啟發性地說明這問題，電子越接近原子核，電子動能越大。但是海森堡不確定性原理不能嚴格給出數學證明，有些特別案例不能滿足第一種穩定性條件，因為量度的是波函數的半寬度，而不是波函數集聚於原子核附近的程度，所以波函數可以擁有一定的半寬度，並且極度集聚於原子核附近，造成庫侖勢能趨於，同時維持有限的動能。

更詳細分析起見，只考慮類氫原子系統，給定原子的原子序Z ，原子的能量 E為

其中，為動能，為勢能，為描述類氫原子系統的波函數， 為位置坐標，為積分體積。

應用索博列夫不等式，經過一番運算，可以得到能量最大下界為

其中， Ry是能量單位里德伯，大約為13.6eV。

總結，類氫原子滿足第一種穩定性條件這結果。

● 氘

● 氚

● 氫原子光譜

● 21公分線

● 量子化學

● 類氫原子

● 球對稱位勢

● 拉普拉斯-龍格-楞次矢量