孤立子
孤立子
又稱孤立子波,是非線性波動方程的一類脈衝狀的行波解。它們的波形和速度在相互碰撞后仍能保持不變或者只有微弱的變化。一個著名的例子是KdV(Korteweg-de Vries) 方程。
目錄
著例(- ) 程 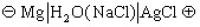 的解
的解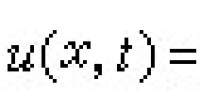
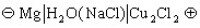 。方程解的圖形(見圖
。方程解的圖形(見圖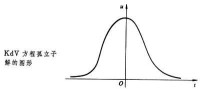 )像一個孤立的脈衝,波峰高2α2,速度為4α2。當兩個這樣的脈衝波沿同一方向運動時,峰高的波速度快會趕上前面峰低的波而發生碰撞。1965年M.D.克魯斯卡爾和N.J.扎布斯基在電子計算機上作數值試驗后,意外地發現兩個這樣的波在碰撞后,居然都能保持各自的波形和速度不變。這一性質使人聯想起粒子,因之將這樣的波稱為孤立子(波)。早在1934年,J.S.羅素已在河流中觀察到這種非線性波。現在人們已經發現很多在應用中十分重要的非線性波方程, 如正弦-戈登方程(SG方程)uxt=sinu,非線性薛定諤方程
)像一個孤立的脈衝,波峰高2α2,速度為4α2。當兩個這樣的脈衝波沿同一方向運動時,峰高的波速度快會趕上前面峰低的波而發生碰撞。1965年M.D.克魯斯卡爾和N.J.扎布斯基在電子計算機上作數值試驗后,意外地發現兩個這樣的波在碰撞后,居然都能保持各自的波形和速度不變。這一性質使人聯想起粒子,因之將這樣的波稱為孤立子(波)。早在1934年,J.S.羅素已在河流中觀察到這種非線性波。現在人們已經發現很多在應用中十分重要的非線性波方程, 如正弦-戈登方程(SG方程)uxt=sinu,非線性薛定諤方程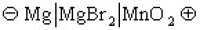
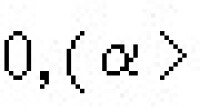
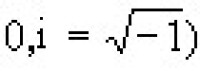 等等都具有這種孤立子解。近年來,發現在等離子體光纖通信中都有孤立子現象,科學家們還認為神經細胞軸突(axon)上傳導的衝動、木星上的紅斑等都可以看作是孤立子。孤立子反映了自然界中一類相當普遍的非線性現象。由於孤立子同時具有波和粒子兩重性質,引起了理論物理學家的極大關注,他們嘗試用它來描寫基本粒子。但在應用中,上述的孤立子的定義,在各種不同意義上有所放寬。
等等都具有這種孤立子解。近年來,發現在等離子體光纖通信中都有孤立子現象,科學家們還認為神經細胞軸突(axon)上傳導的衝動、木星上的紅斑等都可以看作是孤立子。孤立子反映了自然界中一類相當普遍的非線性現象。由於孤立子同時具有波和粒子兩重性質,引起了理論物理學家的極大關注,他們嘗試用它來描寫基本粒子。但在應用中,上述的孤立子的定義,在各種不同意義上有所放寬。
孤立子
孤立子
孤立子

孤立子
孤立子
孤立子
孤立子
求具孤殊非線性方程,自1967年起發展了一種散射反演方法。該方法的特色是將這類非線性問題的解轉化為線性問題來求解,最初是C.S.伽德納等人於1967年首先對KdV方程提出的。他們發現KdV方程和常微分運算元的特徵值問題 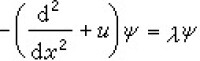 有密切的關係。特別,若微分運算元
有密切的關係。特別,若微分運算元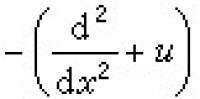 中所含u(稱為位勢)取為KdV方程的解時,運算元的特徵值λ與時間t無關。於是,求解KdV方程的初值問題可以轉化為求解上述特徵值問題的正問題和反問題。其正問題是指已知初值u(x,0)=ƒ(x)求出與運算元
中所含u(稱為位勢)取為KdV方程的解時,運算元的特徵值λ與時間t無關。於是,求解KdV方程的初值問題可以轉化為求解上述特徵值問題的正問題和反問題。其正問題是指已知初值u(x,0)=ƒ(x)求出與運算元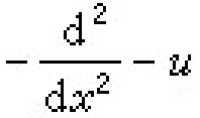 的特徵值等相關的一組量。這一組量稱為散射量。其反問題是指已知t時刻的散射量來複原位勢u(x,t)。散射量本身隨時間t的演化規律十分簡單,關鍵的步驟是求解反問題,而這一步歸結為求解一個線性積分方程。伽德納等人用這種方法成功地求出了KdV方程的單個孤立子解以及由N個孤立子疊加起來的N重孤立子解。1968年 P.D.拉克斯對伽德納等人的思想從泛函分析的角度作了十分清楚的表述,指出KdV方程可以寫成lt=【A,l】形式,其中【A,l】=Al-lA,l和 A為與u有關的線性常微分運算元。由於它在孤立子理論中的重要作用,後人便將它稱作拉克斯方程,並將其l和A稱為拉克斯對。此後又有許多人考察了一類二階矩陣常微分運算元的特徵值問題,導出了與之相連的一族廣泛的非線性演化方程,並建立了與該特徵值問題的反問題相關連的線性積分方程。自此以後,散射反演方法逐漸發展成一種求解非線性方程初值問題的系統方法,引起了數學界的廣泛重視。
的特徵值等相關的一組量。這一組量稱為散射量。其反問題是指已知t時刻的散射量來複原位勢u(x,t)。散射量本身隨時間t的演化規律十分簡單,關鍵的步驟是求解反問題,而這一步歸結為求解一個線性積分方程。伽德納等人用這種方法成功地求出了KdV方程的單個孤立子解以及由N個孤立子疊加起來的N重孤立子解。1968年 P.D.拉克斯對伽德納等人的思想從泛函分析的角度作了十分清楚的表述,指出KdV方程可以寫成lt=【A,l】形式,其中【A,l】=Al-lA,l和 A為與u有關的線性常微分運算元。由於它在孤立子理論中的重要作用,後人便將它稱作拉克斯方程,並將其l和A稱為拉克斯對。此後又有許多人考察了一類二階矩陣常微分運算元的特徵值問題,導出了與之相連的一族廣泛的非線性演化方程,並建立了與該特徵值問題的反問題相關連的線性積分方程。自此以後,散射反演方法逐漸發展成一種求解非線性方程初值問題的系統方法,引起了數學界的廣泛重視。
孤立子
孤立子
孤立子
除散射反演,貝隆換,程另換。程凡(u=0)出發,經簡單積分或代數運算導出方程的一系列特解。一個經典例子是Bα:u0→u1,這裡u1是由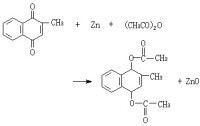 ,
,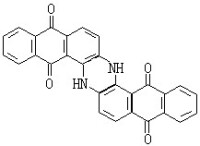
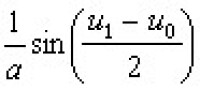 確定的。只要u0是SG方程的解,則由上式可解出u1,它也是SG方程的解。式中α為自由參數。特別,取平凡解u0=0,可解得
確定的。只要u0是SG方程的解,則由上式可解出u1,它也是SG方程的解。式中α為自由參數。特別,取平凡解u0=0,可解得 ,這是SG方程的一種孤立子解,稱之為扭,解中的正負號分別代表兩種相反的旋轉方向(正扭與反扭)。貝克隆變換的一個重要性質是它的可交換性
,這是SG方程的一種孤立子解,稱之為扭,解中的正負號分別代表兩種相反的旋轉方向(正扭與反扭)。貝克隆變換的一個重要性質是它的可交換性 ,其中Bα表示參數為α的貝克隆變換。由此性質可以導出解的非線性疊加公式:
,其中Bα表示參數為α的貝克隆變換。由此性質可以導出解的非線性疊加公式: ,其中
,其中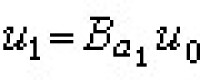 ,
,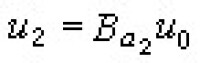 ,
,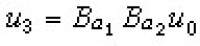 。取u0=0時的u1,u2即為上述的“扭”孤立子解,代入上面的疊加公式就得SG方程的兩重孤立子解
。取u0=0時的u1,u2即為上述的“扭”孤立子解,代入上面的疊加公式就得SG方程的兩重孤立子解

孤立子

孤立子
孤立子

孤立子

孤立子

孤立子
孤立子
孤立子
孤立子
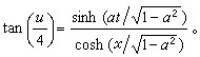
孤立子
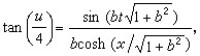
孤立子
散射反演方法之所以獲得成功,是因為它所處理的這類方程都可以寫成一對線性方程 ψx=Uψ與ψt=Vψ的可積條件ψxt=ψtx,亦即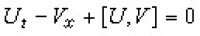 ,這裡U、V是某些方陣。凡是可以作為這樣的關於ψ的線性方程組的可積條件的非線性方程,稱為可積型的。
,這裡U、V是某些方陣。凡是可以作為這樣的關於ψ的線性方程組的可積條件的非線性方程,稱為可積型的。
孤立子