中位線
一種線的定義
中位線是一個數學術語,是平面幾何內的三角形任意兩邊中點的連線或梯形兩腰中點的連線。
三角形:連接三角形兩邊中點的線段叫做三角形的中位線。三角形的中位線平行於第三邊,其長度為第三邊長的一半,通過相似三角形的性質易得。其兩個逆定理也成立,即經過三角形一邊中點平行於另一邊的直線,必平分第三邊;以及三角形內部平行於一邊且長度為此邊一半的線段必為此三角形的中位線。但是注意過三角形一邊中點作一長度為底邊一半的線段有兩個,不一定與底邊平行。
梯形:連接梯形兩腰中點的線段叫做梯形的中位線。梯形的中位線平行於上底和下底,其長度為上、下底長度和的一半,可將梯形旋轉180°、將其補齊為平行四邊形后易證。其逆定理正確與否與上相仿。
連接三角形兩邊中點的線段叫做三角形的中位線,三角形的中位線平行於第三邊並且等於第三邊邊長的一半。
連接梯形兩腰中點的線段叫做梯形的中位線,梯形的中位線平行於兩底,並且等於兩底的一半。
(1)三角形中位線定義:連接三角形兩邊中點的線段叫做三角形的中位線。
(2)梯形中位線定義:連接梯形兩腰中點的線段叫做梯形的中位線。
注意:
(1)要把三角形的中位線與三角形的下位下位區分開。三角形中線是連接一頂點和它對邊的中點,而三角形中位線是連接三角形兩邊中點的線段。
(2)梯形的中位線是連接兩腰中點的線段而不是連接兩底中點的線段。
(3)兩個中位線定義間的聯繫:可以把三角形看成是上底為零時的梯形,這時梯形的中位線就變成三角形的中位線。
三角形中位線定理:三角形的中位線平行於第三邊並且等於它的一半.
如圖,三角形兩邊中點的連線(中位線)平行於第BC邊,且等於第三邊的一半。
三角形的中位線所構成的小三角形(中點三角形)面積是原三角形面積的四分之一。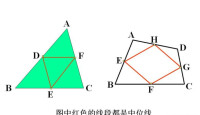

中位線
證明
例題
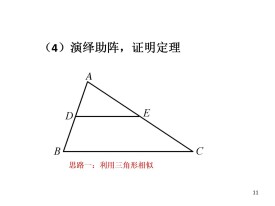
如圖1,已知中,D,E分別是AB,AC兩邊中點。
求證DE平行且等於
法一:過C作AB的平行線交DE的延長線於F點。
∴BCFD是平行四邊形
∴在平行四邊形
∴三角形的中位線定理成立.
法二:利用相似證
∵D,E分別是AB,AC兩邊中點
又
法三:坐標法
設三角形三點分別為
則一條邊長為:根號
另兩邊中點為
這兩中點距離為:根號
最後化簡時將x3,y3消掉正好中位線長為其對應邊長的一半
其他題目
已知:在中,中位線EF與中線AD相交於點O,
求證:AD與EF互相平分.
證明:連接DE、DF,
,
同理得,
,
.
逆定理一:
如圖,則D是AB的中點,E是AC的中點。
逆定理二:
如圖D是AB的中點,,則E是AC的中點,
【證法①】
取AC中點G,聯結DG
則DG是三角形ABC的中位線
又
∴DG和DE重合(過直線外一點,有且只有一條直線與已知直線平行)
(2)梯形中位線定理:梯形的中位線平行於兩底,並且等於兩底和的一半。
中位線是三角形與梯形中的一條重要線段,由於它的性質與線段的中點及平行線緊密相連,因此,它在幾何圖形的計算及證明中有著廣泛的應用。
梯形的中位線平行於兩底,並且等於兩底和的一半.梯形中位線的2倍乘高再除以二就等於梯形的面積,用符號表示是L。
已知中位線長度和高度,就能求出梯形的面積.
中位線在關於梯形的各種題型中都是一條得天獨厚的輔助線。
四邊形ABCD是梯形,,E、F分別是AB、CD邊上的中點,求證:
梯形中位線
證明:
連接AF並延長交BC的延長線於G。
三角形三條中位線所構成的三角形與原三角形相似。