互易定理

互易性質表現為：將網路的輸入和特定輸出互換位置后，輸出不因這種換位而有所改變。具有互易性質的網路稱為互易網路。互易性不僅一些電網路有，某些聲學系統、力學系統等也有。互易定理是一個較有普遍意義的定理。

時域表述 對一個互易二埠網路NR，在時域中互易定理有3種表述。

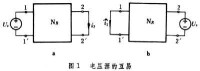
表述一：在NR的入口接入電壓源時，其出口處的短路零狀態響應為（圖1a）；若將電壓源改接在出口上，則出現在入口處的短路零狀態響應嫆（圖1b）恆與相等，即

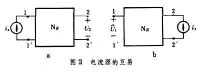
表述二：設在NR的入口接入電流源id時，其出口處的開路零狀態響應為（圖2a）；若將電流源改接在出口上，則出現在入口處的開路零狀態響應（圖2b）恆與相等，即

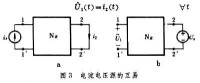
表述三：在NR的入口接入電流源時，其出口處的短路零狀態響應為（圖3a）；若在出口處接上一個與電流源id波形相同的電壓源，則出現在入口處的開路零狀態響應（圖3b）恆與的波形相同，即　

復頻域表述 在復頻域中電壓、電流可用各自的拉普拉斯變換（即象函數）來表示。於是，從互易定理在時域中的表述導出它在復頻域中的表述為：對於互易二埠網路NR，下列關係恆成立，即

前兩式表明互易二埠網路的Y 參數矩陣和Z 參數矩陣是對稱矩陣，后式表明互易二埠網路的H 參數矩陣是反對稱矩陣。

將上列諸式中的變數S換成就得到正弦穩態下的互易定理。

應用條件 並非任何一個網路都具有互易性質。一般地說，由線性時不變的二端電阻元件、電感元件、電容元件、耦合電感器和理想變壓器連接而成的網路均有此性質。含有受控電源、非線性元件、時變元件、迴轉器的網路都不一定具有這種性質。