理想變壓器
沒有功率損耗的理想電路元件
理想變壓器是一個埠的電壓與另一個埠的電壓成正比,且沒有功率損耗的一種互易無源二埠網路。它是根據鐵心變壓器的電氣特性抽象出來的一種理想電路元件。
理想變壓器是一種理想的基本電路元件。為了易於理解,我們從耦合電感的極限情況來引出它的定義。是耦合係數為1的一對耦合電感,圖中N1,N2分別為初級與次級線圈的匝數。定義n=N2/N1,n稱為變比,也稱匝比。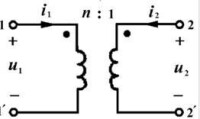

理想變壓器
表徵理想變壓器埠特性的VCR方程是兩個線性代數方程,因而理想變壓器是一種線性雙口電阻元件。正如二端線性電阻元件不同於實際電阻器,理想變壓器這種電路元件也不同於各種實際變壓器。例如用線圈繞制的鐵心變壓器對電壓、電流的工作頻率有一定限制,而理想變壓器則是一種理想化模型。它既可工作於交流又可工作於直流,對電壓、電流的頻率和波形沒有任何限制。將一個含變壓器的實際電路抽象為電路模型時,應根據實際電路器件的情況說明該模型適用的範圍。
理想變壓器的有四個理想化條件:
(1)無漏磁通,即Φs1=Φs2=0,耦合係數K=1,為全耦合,故有Φ11=Φ21,Φ22=Φ12。
(2)不消耗能量(即無損失),也不貯存能量。
磁滯現象是導磁材料的一種特性,當變壓器線圈里有交流電流時,就會產生交變磁場,這個交磁滯現象變磁場反覆對鐵芯進行磁化,由於鐵芯有一定的磁阻,在磁化過程中就有磁滯現象,這種由磁滯現象所引起的能量損耗,叫做磁滯損耗。再者,當變壓器的原線圈通電后,線圈所產生的磁通在磁芯中流動,由於鐵芯本身是導體,在垂直於磁感線的平面上就會產生感應電動勢,這個電動勢在鐵芯的斷面上形成閉合迴路併產生電流,就像漩渦一樣,我們把這個電流稱為“渦流”。“渦流”使變壓器的鐵芯發熱,溫度升高,這種損耗稱為“渦流損耗”。變壓器的磁滯損耗和渦流損耗統稱為“鐵耗”。若是理想變壓器,其鐵芯屬於軟磁材料,磁導率認為無窮大,磁阻趨於零,磁滯損耗可以忽略;同時也要忽略渦流損耗。
變壓器的線圈存在著電阻,電流流過電阻時會產生熱量,要消耗一定的功率,我們稱這種損耗為“銅損”。當變壓器副線圈短路時,副線圈的電流很大,導致原線圈的電流也很大,在線圈電阻上消耗的功率不能忽略,這時的變壓器不能認為是理想變壓器。
變壓器發熱主要是由鐵損和銅損造成的。由於變壓器存在著鐵損和銅損,所以它的輸出功率永遠小於輸入功率。但對理想變壓器而言,不計鐵損和銅損,即不消耗能量,也不儲存能量,認為輸入功率等於輸出功率。
(4)因有K=1,L1→∞,L2→∞,故有M→∞。
滿足以上四個條件的耦合電感稱為理想變壓器。可見理想變壓器可認為是耦合電感的極限情況。即K=1,L1→∞,L2→∞,M→∞的情況,它純粹是一種變化信號的傳輸電能的元件,但它與耦合電感在本質上已不同了。耦合電感是依據電磁感應原理工作的,是動態元件,需要三個參數L1,L2,M來描述;而理想變壓器已沒有了電磁感應的痕迹,是靜態元件,只需要一個參數n來描述。。理想變壓器是電路的基本無源元件之一。工程實際中使用的鐵心變壓器,在精確度要求不高時,均可用理想變壓器作為它的電路模型來進行分析與計算。
簡而言之,理想變壓器就是無磁損無銅損無鐵損的變壓器。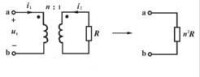

理想變壓器
理想變壓器有兩個基本性質:
1.理想變壓器既不消耗能量,也不儲存能量,在任一時刻進入理想變壓器的功率等於零,即p=u1i1+u2i2=nu2i1+u2ni1
此式說明從初級進入理想變壓器的功率,全部傳輸到次級的負載中,它本身既不消耗,也不儲存能量。
2.當理想變壓器次級端接一個電阻R時,初級的輸入電阻為n2R。
U1:U2=N1:N2(理想變壓器電壓之比與線圈匝數成正比)
I1:I2=N2:N1(理想變壓器電流之比與線圈匝數成反比)
由於無漏磁通,故穿過兩個線圈的總磁通相同,均為Φ=Φ21+Φ12=Φ11+Φ22。又由於圖中u1(t),i1(t)和Φ三者的參考方向互為關聯,u2(t),i2(t)和Φ三者的參考方向也互為關聯,故:u1(t)=N1dΦ/dt u2(t)=N2dΦ/dt故有u1(t)/u2(t)=N1/N2=1/n(7-6-1a)或 u1(t)=u2(t)/n(7-6-1b)又因為理想變壓器不消耗也不貯存能量,所以它吸收的瞬時功率必為零,即必有 u1(t)i1(t)+u2(t)i1(t)=0故得 i1(t)/i2(t)=-u2(t)/u1(t)=-N2/N1=-n (7-6-2a)或 i1(t)=-ni2(t) (7-6-2b)式(7-6-1),(7-6-2)即為理想變壓器的時域伏安方程。可看出:1.由於n為大於零的實數,故此兩方程均為代數方程。即理想變壓器為一靜態元件(無記憶元件),已經沒有了電磁感應的痕迹,所以能變化直流電壓和直流電流。2.理想變壓器的兩線圈的電壓與其匝數成正比,兩線圈的電流與其匝數成反比,且當n;1時有u2(t);u1(t),為升壓變壓器;當n<;1時有u2(t)<;u1(t),為降壓變壓器;當n=1是有u2(t)=u1(t),既不升壓也不降壓。3.在電路理論中,我們把能聯繫兩種電路變數的元件稱為相關元件,否則即為非相關性元件。電阻,電感,電容等均為相關性元件,而理想變壓器則為非相關性元件,亦即u1(t)與i1(t)之間,u2(t)與i2(t)之間,均無直接的約束關係,它們均各自由外電路決定。當電路工作在正弦穩態時,式(7-6-1),(7-6-2)即可寫為向量形式,即式(7-6-1)和(7-6-2)均是在圖示電壓參考極性與電流參考方向以及同名端標誌下列出的。若線圈的同名端或電壓的參考極性,電流的參考方向改變了,則其伏安方程中等號右端的"+","-"號也應相應改變。例如對於圖7-6-2(a).(b)所示電路,則其伏安方程為;圖7-6-2理想變壓器電路(a)同名端改變(b)i2(t)參考方向和u2(t)參考極性改變需要指出,從耦合電感的極限來定義理想變壓器只是一種方法,是為了使讀者易於接受。理想變壓器的本質定義應是從數學上來定義,即凡滿足式(7-6-1),(7-6-2)伏安方程的電路元件即為理想變壓器,其電路符號採用圖7-6-1(b),(c)表示,也只是因襲了傳統而已,並非一定要由線圈構成。
設在理想變壓器的次級接阻抗Z,如圖示,則應有;故得原邊的輸入阻抗為
於是可得原邊等效電路如圖7-6-3(b)所示。從式(7-6-4)看出:(1) n≠1時,Z0≠Z,這說明理想變壓器具有阻抗變換作用。n;1時,Z0;Z; n<;1時,Z0<;Z。
p;圖7-6-3理想變壓器的阻抗變換作用(2)由於n為大於零的實常數,故Z0與Z的性質全同,即次級的R,L,C,變換到初級相應為R/n2,L/n2,n2C。(3)阻抗變換與同名端無關。(4)當Z=0時,則Z0=0,即當次級短路時,相當與初級也短路。(5) Z=∞時,則Z0=∞,即當次級開路時,相當與初級開路。 (6)阻抗變換具有可逆性,即也可將原邊的阻抗Z變換到副邊,如圖7-6-4所示。但要注意此時副邊的等效阻抗為Z0=n2Z。
圖7-6-4阻抗變換作用的可逆性(7)阻抗在某一邊是串聯(並聯),則變換到另一邊也是串聯(並聯),如圖7-6-5所示。
;圖7-6-5理想變壓器阻抗變換作用的性質由以上的全部敘述可見,理想變壓器既能變換電壓和電流,也能變換阻抗,因此,人們更確切地稱它為變數器。
在電子線路中,常利用理想變壓器的阻抗變換作用來實現阻抗匹配,使負載獲得最大功率。
用受控源模擬理想變壓器將式(7-6-1),(7-6-2)改寫為
根據此兩方程即可將理想變壓器用受控源電路來模擬,相應如圖7-6-6所示。