格林函數
格林函數
在數學中,格林函數是一種用來解有初始條件或邊界條件的非齊次微分方程的函數。在物理學的多體理論中,格林函數常常指各種關聯函數,有時並不符合數學上的定義。從物理上看,一個數學物理方程是表示一種特定的"場"和產生這種場的"源"之間的關係。例如,熱傳導方程表示溫度場和熱源之間的關係,泊松方程表示靜電場和電荷分佈的關係,等等。這樣,當源被分解成很多點源的疊加時,如果能設法知道點源產生的場,利用疊加原理,我們可以求出同樣邊界條件下任意源的場,這種求解數學物理方程的方法就叫格林函數法。而點源產生的場就叫做格林函數。
格林函數法是數學物理方程中一種常用的方法。
格林函數是物理學中的一個重要函數。在數學物理方法中,格林函數又稱為源函數或影響函數,是英國人G.格林於1828年引入的。
物理學中單體量子理論所使用的格林函數,其定義稍有擴充。它滿足方程:(E-H)G(r,rt,E)=(r-rt),其中H是單粒子哈密頓量,可以包括外場及雜質勢等。單格林函數在無序體系研究中有重要應用,例如用平均T矩陣近似、相干勢近似求態密度。
多體量子理論的格林函數自20世紀60年代以來已成為凝聚態理論研究的有力工具。物理當中格林函數常指用於研究大量相互作用粒子組成的體系的多體格林函數。多體格林函數代表某時某地向體系外加一個粒子,又於它時它地出現的幾率振幅。格林函數描寫粒子的傳播行為,又稱為傳播子。
為了研究多粒子體系在大於絕對零度時的平衡態行為,引入了溫度格林函數。由於溫度的倒數和虛時間有形式上的對應,溫度格林函數也稱為虛時間格林函數。為了研究T=OK的非平衡態行為,[kg2]引入了T=OK的時間格林函數及閉路格林函數。
在量子場論中計算具體物理過程的矩陣元時,也常出現格林函數,其物理意義也是代表粒子傳播的幾率振幅。由於多體格林函數T=OK時對應於它,所以量子場論中的費因曼圖解法(見費因曼圖)也可用於多體格林函數。重正化群方法來也用於凝聚態研究中,例如近藤效應、一維導體。
給定流形M上的微分運算元L,其格林函數
,為以下方程的解
格林函數
其中
若L的零空間非平凡,則格林函數不唯一。不過,實際上因著對稱性、邊界條件或其他的因素,可以找到唯一的格林函數。一般來說,格林函數只是一個廣義函數。
格林函數在凝聚態物理學中常被使用,因為格林函數允許擴散方程式有較高的精度。在量子力學中,哈密頓運算元的格林函數和狀態密度有重要的關係。由於擴散方程式和薛定諤方程有類似的數學結構,因此兩者對應的格林函數也相當接近。
在時域測量中,由於無限短的脈衝激勵源可視為組織體邊界下自由傳輸深度ls處的彌向的無限短脈衝點源(光子在t=0時刻同時入射),該衝擊響應也因此被稱為格林函數。格林函數對於解線性系統在實際光源激勵下的響應問題具有很重要的意義。如果實際的光源為具有一定強度空間分佈、時間分佈、角度分佈的光源,則此光源下的系統響應可表示為格林函數與光源分佈函數的乘積在全空間、角度和時間域的積分。
例如,假設投射到組織體表面的光源的光子密度分佈為q(r,s’,t),系統的格林函數為G(r,s’,t),則q(r,s’,t)下系統的響應為
為區別起見在後續將格林函數統一用G(r,t)表示,由於關於
的格林函數表示為
,於是時變擴散方程
有
(3.56)
對於均勻媒質,上述方程的頻域形式
可表示為
(3.57)
在式(3.56)中令
或在式(3.57)中令
,即得穩態(或直流)擴散方程。對於均勻媒質,穩態(或直流)擴散方程表示為
。
作為其餘各解析求解的基礎,下面將首先建立無限媒質中的光學響應。為此,對式(3.57)兩邊取三維空間傅立葉變換
(3.58)
式中,s為頻域空間矢量。對式(3.58)求空間的傅里葉逆變換,得
(3.59)
根據
,並令r的方向與s之
方向一致,有
(3.60)
式中,
,
,
。
考慮到
,所以
。進一步得
(3.61)
式中被積函數為偶函數,且在複平面有兩個一階極點:
,分別位於上下半平面,其中第一項
時趨於零,因此圍道積分應在下半平面進行;反之式(3.61)第二項圍道積分應在上半平面進行,於是根據留數定理
(3.62)
對上式求傅里葉反變換,得時域無限均勻媒質下的格林函數
(3.63)
於是由式(3.63)和式(3.54)可得
(3.64)
格林函數
為r方向單位矢量。當連續以一定的速率注入光子,即穩態時,無線均勻媒質下的格林函數為
(3.65)
式中
稱為有效衰減係數。
稱為穿透深度。
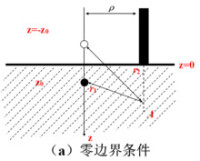
對於如圖3.8所示的半無限空間,格林函數可利用上述全空間解和鏡像原理求得。我們仍然假定各向同性點光源位於組織體表面下
處。下面介紹鏡像源的添加原理。
格林函數
如圖3.8(a),在物理邊界上採用Dirichlet邊界條件,可在z<0半空間填充媒質並在
處加入負鏡像點源。則根據唯一性原理,此時z=0區域的解與原問題解相同,則可實現半無窮空間的零邊界條件,這樣實際的物理邊界就可以移去,從而可根據全空間的解式(3.63)可得半無窮空間任意一點A處(r=(x,y,z))的解
(3.66)
式中,
。
和
為
和
向的單位矢量,根據Fick原理,在邊界上(z=0)距源的距離為
的點測得到的漫反射光流量為
(3.67)
當
時,從式(3.67)可以得到
(3.68)
(3.69)
式(3.69)說明,吸收係數可以通過對
對t的曲線在t為無窮大時的斜率得到。另外擴散係數也可以通過
的最大點計算得到。由於在
與t的關係曲線上,頂點處斜率為零,如果設此時對應的時間為
並考慮到
,則根據式(3.68)可得
(3.70)
格林函數
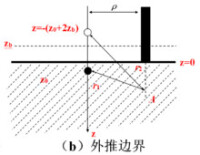
(2)外推邊界情況下
在外推邊界條件下,物理邊界可以通過在外推邊界上部的
處放置鏡像源而移去,見圖3.8(b)。參考零邊界條件的推導結果,相應地,對於外推邊界條件
(3.71)
根據Fick定律,組織體表面的檢測光流量為
(3.72)
式中
,
,
。
格林函數
的點測得的反射光強為
(3.73)
厚度為d的無限組織層格林函數同樣可利用全空間解和鏡像原理求得。設激勵點光源位於組織體表面下
處,為了使光子密度在z=0處滿足Dirichlet邊界條件(不考慮外延邊界)應在1'處加鏡像元。為了在z=d處滿足Dirichlet邊界條件,應在2和2'處加鏡像源用來分別抵消1和1'在z=d處的影響。而應在2和2'處加鏡像源后又會造成z=0邊界不滿足邊界條件,所以應在
放置無窮個鏡像點源偶極子,如圖3.9所示。於是很容易寫出:
①z=0處的反射通量密度
(3.74)
式中
,
。
②z=d處的反射通量密度
格林函數
式中
,
。
·穩定問題的格林函數也可以利用靜電場 類比法得到。
·點源問題可以看成接地的導體邊界內在 r’ 處有一個 電量為 - ε0 的 點電荷。
·邊界內部的電場由 點電荷與導體中的感應電荷共同產生。
·在一些情況下,導體中所有感應 電荷的作用可以用一個設想的等效電荷來代替,該等效電荷稱為 點電荷的電像。
·這種方法稱為電像法
格林函數在地震工程學中是計算震源機制的函數。根據其發展和應用可以分為以下幾類
。
隨機法是將地震動模擬成有限帶寬白雜訊的一個時間序列,用震源譜代震級、用表示地震波傳播效應因子修正譜的形狀。對於大地震,震源表達為在一個延伸的斷裂面上的剪切位錯,斷裂面上的滑動空間和時間變化用離散的方法表示。其優點是對於高頻段(>1Hz)可以得到滿足工程要求的近場地震動估計;缺點是對於低頻段(<1Hz)往往估計過高
。
經驗格林函數法是運用包含斷層上一個點源動力學破裂的複雜效應、震源主場地速度結構的不均勻性影響的小震記錄來疊加合成較大地震的地震動時程。其優點是信度較高、較為可靠;可是其缺點同樣突出,即對小震記錄的要求相當苛刻,必須具有與大震相同的震源機制,小震記錄的信噪比要高等等。如果在震源區找不到良好的小震記錄,就不能用經驗格林函數法。
理論格林函數的計算是一個相當複雜的過程,理論只有對水平成層介質推導的解析公式。計算要藉助計算機實現,且介質層數受到很大的限制,很少有多於兩復蓋層的結果發表。
與實際地震動觀測記錄的比較表明,這種在時域合成的地震動模擬,對持時、峰值加速度、短周期(1秒以下)反應譜幅值的預測精度都可以在大約-50%範圍內,與經驗模型的精度大體相當;對峰值速度和周期大於1秒的反應譜幅值,預測的誤差要比經驗模型的小。
除了以上介紹的幾種格林函數的數值方法,還有解析法
。解析法只能用來計算橫向成層介質的格林函數,再考慮計算時間及計算方法的穩定性方面計算的層數是優先的,對較複雜的局部場地條件則無能為力。張冬麗在對格林函數的解析法和數值法對比研究后得出以下結論:
(1)無論是單一點源或是有限斷層模型,利用解析法和有限差分法所得出的結果是一致的,二者均可以反映出震源、波的傳播途徑和場地特性(斷裂和上復蓋層速度結構)。
(2)解析法用於橫向成層介質的格林函數較為簡便,對於地形及速度結構較為複雜的局部場地條件的格林函數,用數值模擬的方法更為合適,故兩種計算方法的結合可為計算較深震源及較大的計算區域打下基礎。
(3)基於射線理論和波動有限元數值模擬,採用雙力偶點源模型計算斷層在斷層頂面引起的地震影響場(解析法),並將其作為斷層上復蓋層的波動有限元數值模擬的入射場,計算(數值法)得到的格林函數是合理的。它可以兼顧波的傳播途徑與場地波速層與地形的複雜性,同時大大減小了計算量,提高了計算速度,也可保證模擬的穩定性和精度,為進一步計算斷層運動在局部場地引起的土層地震反應提供了必不可少的條件。
強震觀測數據分析表明,在高頻和低頻兩個不同頻段內,地震動特徵顯著不同。高頻段充分表現地震動的隨機性,低頻段主要受傳播途徑和局部場地條件的影響。根據上述幾種格林函數方法的優缺點,選擇用隨機法估計得高頻地震動和用理論或數值格林函數方法模擬的低頻的地震動在時域疊加,是現今對於格林函數方法模擬和預測地震動的發展趨勢。
