垂線公理
適用於數學領域的定理
直線外一點與直線上各點連接的所有線段中,垂線段最短(簡稱“垂線段最短”)。
如垂線段圖,已知於點C,則。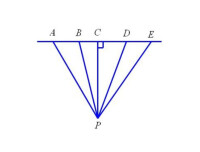

垂線公理
在同一平面內,過一點(直線上或直線外)有且只有一條直線與已知直線垂直。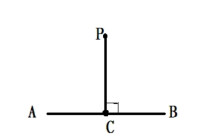

垂線公理
如垂直圖,過直線AB上一點C作,且CP是唯一的;同理,過直線AB外一點P作,且PC是唯一的。
當兩條直線相交所成的四個角中,有一個角是直角時,即兩條直線互相垂直,其中一條直線叫做另一直線的垂線,交點叫垂足。
垂線段是一個圖形,點到直線的距離是一個數量。
已知直線AB和平面內一點C,過C作AB的垂線,求證這樣的直線有且只有一條。
證明:當C在直線上時,作,,不妨設CD在CD'的左邊,則∠D'CB在∠DCB的內部。
而
,小的等於大的,這是不可能的事情。
∴假設不成立,即當C在AB上時,有且只有一條直線CD與AB垂直。
當C在直線外時,作,垂足分別為D、D'。
則
根據同旁內角互補,兩直線平行可知,,這和CD與CD'交於C矛盾。
∴假設不成立,即當C在直線外時,有且只有一條直線CD與AB垂直。
這樣就證明了,無論C是否AB上,命題都成立。
已知直線AB和直線外一點C。作,垂足為D。連接C與AB上異於D的任意一點E,求證。
證明:由定理的第一部分可知CD是唯一的垂線段,那麼C、D、E就構成了以∠CDE為直角的Rt△CDE。
由三角形內角和定理可知,△CDE內沒有比∠CDE更大的角
大角對大邊,因此
由E的任意性可知對於任一異於D的E,都有,即垂線段最短。
