分子反應動力學
分子反應動力學
分子反應動力學(Molecular Reaction Dynamics)又稱微觀反應動力學。是從原子、分子的微觀性質出發,分析分子間的運動及其相互作用,從而深刻地認識化學反應的本質及其規律的一門學科。分子反應動力學研究建立在現代物理有關分子、原子、激光與激光理論、分子束、能譜等實驗技術及電子計算機技術基礎之上。它應用現代物理化學的先進分析方法,在原子、分子的層次上研究不同狀態下和不同分子體系中單分子的基元化學反應的動態結構,反應過程和反應機理。這一研究深入到分子或原子的微觀層次,研究不同能態(平動、振動、電子運動)、不同構型的分子反應特徵。研究分子內部運動和分子之間的碰撞規律。分子反應動力學研究的實驗方法主要有:交叉分子束實驗技術、激光誘導熒光、化學發光技術等,理論上要解決這樣一些問題:給出反應物分子在空間上的勢能面,即確定反應體系中各反應物分子在空間不同位置上的相互作用;計算作為反應物初態、產物終態函數的反應幾率或反應截面;按反應初態能量分佈規律,從反應截面計算反應速率常數並給出宏觀反應動力學方面的信息。
化學動力學的一個分支,是研究化學反應基元過程分子機理的學科。它用理論物理的方法計算處於某一量子態的分子進行單次碰撞併發生化學反應的幾率(或截面)和產物分子的量子態、空間分佈及反應速率常數等。這些研究提供了如何控制和利用化學反應的理論依據。
例如,為了使吸能反應 I+HCl─→HI+Cl能夠發生,增加 HCl的振動能比增加其平動能更為有效。它的逆反應 Cl+HI─→HCl+I是一個放能反應,分子反應動力學能夠提供產物分子HCl振動態“布居反轉”的信息,從而為尋找化學激光工作物質提供了依據。它還能提供反應體系“碰撞對”真實碰撞過程的信息──“碰撞對”是直接反應還是經過一個絡合物的反應。
理論計算方法:20世紀30年代,以美國物理化學家H.艾林為代表的學派,用海特勒-倫敦計算H2的方法建立了H+H2反應體系的第一個勢能面,藉助統計力學方法計算了在該勢能面上的熱平衡反應速率常數,稱為絕對反應速率理論或過渡態理論。
分子反應動力學的理論計算方法分為三部分:①化學反應體系勢能面的量子化學計算;②反應截面(或幾率)的計算;③由反應截面計算反應速率常數。因此,也可以說分子反應動力學是研究反應體系在熱能面上運動過程的學科。在確定的勢能面上求解核的運動方程,既可以用經典力學方法,也可以用量子力學方法。
分子反應動力學
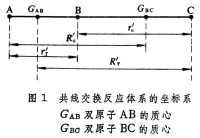
以A+BC─→AB+C雙分子共線交換反應為例 (共線反應是指反應體系的三個原子沿直線相互接近的反應),該反應體系的坐標系見圖1。
在非相對論近似下,反應體系的哈密頓算符 H寫作(圖2):
式中 μA,BC和 μBC分別為A和BC,B和C之間相對運動的約化質量; mA、 mB、 mC分別為原子A、B、C的質量; h為普朗克常數; Vα和 Vγ為有效勢函數。
核運動的薛定諤方程為: Hψ= Eψ (3)
漸近條件為:(圖3)式中α為反應體系的初始排布,即A+BC; nα或 n為BC的內量子數, nα為始態, n為反射態;γ表示終態排布,即C+AB; n為AB分子的內量子數,每一種排布和分子的一組內量子數(如α, nα)稱為反應體系的一個通道; kα或 kγ為原子與雙原子分子相對運動的波數(圖4);
為雙原子分子的內態波函數(圖5);
稱為散射幅。能量守恆條件要求(圖6): (5)
式中啚= h/2π; E為能量。由入射波和出射波幾率流密度守恆的條件,就可以得到由通道(α, nα)到通道(λ, nλ)的反應幾率為(圖7):式中 v為( λ, nλ)通道中反應體系的相對運動速度。
H+H2( n)─→H2+H共線交換反應幾率的數值計算結果見圖2。
對於實際的三維化學反應,用上面的方法可以得到反應截面隨碰撞能變化的關係。用量子散射理論求反應截面(或幾率)的關鍵是求散射幅,一般是在自然反應坐標中用數值求解耦合微分方程。這是一項十分複雜的計算工作。
當反應體系的質量較大,德布羅意波長很短時,用經典軌跡法或者用准經典軌跡法,即對反應物初態分佈和產物終態分佈作量子校正的經典軌跡法研究反應體系沿勢能面的運動,往往也能得到比較滿意的定性或半定量的結果。
由於分子反應動力學的深入發展,對分子反應散射的研究引起了人們極大的興趣。一方面,分子化學反應的實驗研究為化學反應機理的研究提供了詳細的信息;另一方面,對反應散射的理論計算,既可以同實驗結果互相對比,又可以給予實驗結果以清楚的物理解釋。例如,對F+H2反應體系的實驗和理論研究,發現了產物分子振動態“布居反轉”現象,導致了化學激光器的產生,從而推動了態-態反應速率的研究,使分子化學反應動力學發展到態-態分子反應動力學的新階段。
R. D. Levine and R. B. Bernstein, Molecular Reaction Dynamics,Oxford Univ.Press,Oxford,1974.
