德魯克公設

在20啦紀50年代，經典塑性理論有了很大發展，主要表現在以下三個方面：

(1)1951年，德魯克(Drucker)提出的材料穩定性假設或德魯克公設；

(2)1952年，德魯克等提出的極限分析的基本定理；

(3)1960年，德魯克提出的正交性條件的概念或關聯流動法則等的建立與發展。

理想塑性體的極限分析理論能更直接地對結構或土體承載力進行評估。穩定材料的概念提供了一個統一的方法和塑性體的應力-應變莢系的廣義觀點。正交性條件的概念提供了塑性應力-應變關係的屈服準則或載入函數之間的必要關聯。所有這些進展為金屬塑性經典理論打下了嚴格的基礎；，也為後來關於土體和混凝土之類的其他工程材料的更複雜的塑性理論的顯著發展打下了基礎，

對於幾種單向拉伸應力-應變曲線，如右圖1所示。在圖1（a）中，應力增量Δσ>0，應變增量Δε>0，材料是強化的。附加應力Δσ作正功，ΔσΔε>0，這類材料稱為穩定材料；在圖1（b）的非穩定區域中，應力增量Δσ<0，應變增量Δε>0；在圖1（c）的非穩定區域中，應力增量Δσ>0，應變增量Δε<0，兩者都有ΔσΔε<0，這類材料稱為非穩定材料。

滿足下麵條件的材料定義為穩定材料：

（1）在施加附加力系的過程中，外力在所產生的位移變化上做正功；

（2）在附加力系施加和卸載的一個完全循環中，外力所作的凈功和由此產生位移的變化為非負值。

設一個應力循環為：考慮一個材料單元體在t=t時受均勻狀態的應力，假設這個應力在屈服面上或面內（如圖2）。從A點出發，一個外力沿著路徑ABC增加應力，AB在屈服面內，當t=t1時，點B剛好在屈服面上，f（σ）=0（B點）；這個應力繼續向外移動，引起屈服面擴展；當t=t2時，應力為σ+dσ，到達載入面外f'上的C點；然後撤去外力，應力狀態沿著彈性路徑CDA回到。

如果以σ表示應力循環（t1≤t≤t3）過程中任一時刻的瞬時應力狀態，那麼，（σ- ）就是附加應力，德魯克公設要求在這一應力循環中，附加應力所作的功為非負，即W≥0。因為彈性變形時全部可逆的，並與從A→B→C→D→A的路徑無關，應力在這個閉合應力循環過程之後，彈性變形作的功為零。在載入循環過程之後只有塑性功作為外力所作的凈功保留下來，考慮到路徑BC是任意的，可以得到穩定循環條件的數學表達式為：

德魯克公設是在塑性加工力學研究中表徵材料強化特性的重要假設，也是判斷材料穩定的準則。根據該公設不僅可以導出材料載入曲面(包括屈服曲面)外凸的重要性質，而且可以建立塑性狀態下的本構方程，即塑性變形的物性方程。

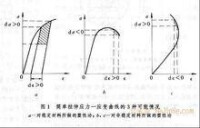
右圖為根據德魯克公設導出的簡單拉伸應力-應變曲線的三種可能情況。

這表明在所有符合屈服條件的應力狀態中，與該塑性應變增量服從增量理論關係的應力狀態(dσ)所耗塑性功最大。可見德魯克公設與最大塑性功原理是等價的。