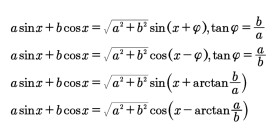輔助角公式
高等三角函數公式
輔助角公式是李善蘭先生提出的一種高等三角函數公式,使用代數式表達為asinx+bcosx=√(a²+b²)sin[x+arctan(b/a)](a>0)。雖然該公式已經被寫入中學課本,但其幾何意義卻鮮為人知。
該公式的主要作用是將多個三角函數的和化成單個函數,以此來求解有關最值問題。
對於型函數,我們可以如此變形
為利用兩角和差公式化簡,
設
使
(注意到a必須>0)
其等價於
則
即
或
如何找出輔助角公式的幾何意義呢?或者說,這個公式中的各個量之間有著怎樣的聯繫呢?
對於這樣一個複雜的公式,不確定的量太多了。
我們需要分析公式中每一個量的意義。
先看等式左邊:兩個分別增大(或減小)一定倍數的正弦與餘弦函數的和。
再看等式右邊:一個增大(或減小)一定倍數並且被改變了初相的正弦函數。
從代數意義上講,輔助角公式是為了對幾個同頻率的正弦型函數求和,轉化為一個單獨的正弦型函數而誕生的。頻率相同意味著相同,所以對於輔助角公式而言,為了方便起見,我們只討論時的特殊情況。在這種情況下,對於一個正弦型函數,我們只有(增大的倍數)與(初相)兩個量需要討論。
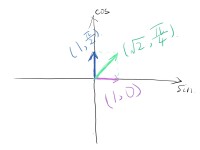
我們可以把看作大小,把看作角度。而角度和大小恰是極坐標系確定位置的兩個要素。
輔助角公式與極坐標系有什麼關係嗎?
簡化問題,使,得
輔助角公式
又因為,則
而在極坐標系中平面向量的加和即為
(如右圖)
兩者之間有異曲同工之妙。
由此可見,我們的猜想得到了一定的驗證。
即與都只是單位向量,而兩者是單位向量的變化幅度,是兩向量和的模,則是和向量與橫軸的夾角。
之前的驗證只是對簡化后的結果進行的,即。其實,這一結果具有普適性。
譬如
你可以自己找幾個例子,多試幾次。
註:這種幾何意義同樣適合推導誘導公式等部分三角函數恆等變換公式,但三角函數間乘法不等價於單位向量間點乘(即數量積)。
----------------------------------------------------------------
另外,該幾何意義也與矩陣有部分聯繫。
即獲得的向量和可以通過該矩陣計算
(以平面直角坐標係為基準,而非極坐標系)
為什麼在推導輔助角公式的時候要令輔助角的取值範圍為?其實是在分類討論a>0或b>0的時候,已經把輔助角的終邊限定在一、四象限內了,此時輔助角的範圍是。而根據三角函數的周期性可知加上后函數值不變,況且在內輔助角可以利用反正切表示,使得公式更加簡潔明了。
李善蘭,原名李心蘭,字竟芳,號秋紉,別號壬叔。出生於1811年 1月22日,逝世於1882年12月9日,浙江海寧人,是中國近代著名的數學、天文學、力學和植物學家,創立了二次平方根的冪級數展開式,研究各種三角函數,反三角函數和對數函數的冪級數展開式(現稱“自然數冪求和公式”),這是李善蘭也是19世紀中國數學界最重大的成就。
求的最大值
解:
設
則
由輔助角公式易得:
整理,得:
令
則
故
又有
易知:
化簡5sina-12cosa
解:5sina-12cosa
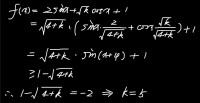
輔助角公式
=13sin(a-b)
其中,cosb=5/13,sinb=12/13
π/6≤a≤π/4 ,求sin²a+2sinacosa+3cos²a的最小值
解:令f(a)=sin²a+2sinacosa+3cos²a
=1+sin2a+2cos²a
=1+sin2a+(1+cos2a)(降冪公式)
=2+(sin2a+cos2a)
=2+(√2)sin(2a+π/4)(輔助角公式)
因為7π/12≤2a+π/4≤3π/4
所以f(a)min=f(3π/4)=2+(√2)sin(3π/4)=3
很多人在利用輔助角公式時,經常忘記反正切到底是b/a還是a/b,導致做題出錯。其實有一個很方便的記憶技巧,就是不管用正弦還是餘弦來表示asinx+bcosx,分母的位置永遠是你用來表示函數名稱的係數。
例如用正弦來表示asinx+bcosx,則反正切就是b/a(即正弦的係數a在分母)。如果用餘弦來表示,那反正切就要變成a/b(餘弦的係數b在分母)。