近似演演算法

所有已知的解決NP-難問題演演算法都有指數型運行時間。但是，如果我們要找一個“好”解而非最優解，有時候多項式演演算法是存在的。

給定一個最小化問題和一個近似演演算法，我們按照如下方法評價演演算法：首先給出最優解的一個下界，然後把演演算法的運行結果與這個下界

進行比較。對於最大化問題，先給出一個上界然後把演演算法的運行結果與這個上界比較。

近似演演算法比較經典的問題包括：最小頂點復蓋、旅行售貨員問題、集合復蓋等。

迄今為止，所有的NP完全問題都還沒有多項式時間演演算法。

對於這類問題，通常可採取以下幾種解題策略。

(1)只對問題的特殊實例求解

(2)用動態規劃法或分支限界法求解

(3)用概率演演算法求解

(4)只求近似解

(5)用啟髮式方法求解

若一個最優化問題的最優值為c*，求解該問題的一個近似演演算法求得的近似最優解相應的目標函數值為c，

則將該近似演演算法的性能比定義為max(c/c*, c*/c)。在通常情況下，該性能比是問題輸入規模n的一個函數

ρ(n)，即 max(c/c*, c*/c) <= ρ(n)。

該近似演演算法的相對誤差定義為Abs[(c-c*)/c*]。若對問題的輸入規模n，有一函數ε(n)使得Abs[(c-c*)/c*] <= ε(n)，則稱ε(n)為該近似演演算法的相對誤差界。近似演演算法的性能比ρ(n)與相對誤差界ε(n)之間顯然有如下

關係：ε(n)≤ρ(n)-1。

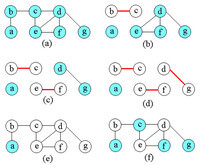
問題描述：無向圖G=(V,E)的頂點復蓋是它的頂點集V的一個子集V’V，使得若(u,v)是G的一條邊，則v∈V’或u∈V’。頂點復蓋V’的大小是它所包含的頂點個數|V’|。

VertexSet approxVertexCover ( Graph g )

{ cset=；

e1=g.e；

while (e1 != ) {

從e1中任取一條邊(u,v)；

cset=cset∪{u,v}；

從e1中刪去與u和v相關聯的所有邊；

}

return c

}

Cset用來存儲頂點復蓋中的各頂點。初始為空，不斷從邊集e1中選取一邊(u,v)，將邊的端點加入cset中，並將e1中已被u和v復蓋的邊刪去，直至cset已復蓋所有邊。即e1為空。

圖(a)～(e)說明了演演算法的運行過程及結果。(e)表示演演算法產生的近似最優頂點復蓋cset，它由頂點b,c,d,e,f,g所組成。(f)是圖G的一個最小頂點復蓋，它只含有3個頂點：b,d和e。

旅行售貨員問題的一些特殊性質：

比如，費用函數c往往具有三角不等式性質，即對任意的3個頂點u,v,w∈V，有：c(u,w)≤c(u,v)+c(v,w)。當圖G中的頂點就是平面上的點，任意2頂點間的費用就是這2點間的歐氏距離時，費用函數c就具有三角不等式性質。

對於給定的無向圖G，可以利用找圖G的最小生成樹的演演算法設計找近似最優的旅行售貨員迴路的演演算法。

void approxTSP (Graph g)

{

(1)選擇g的任一頂點r；

(2)用Prim演演算法找出帶權圖g的一棵以r為根的最小生成樹T；

(3)前序遍歷樹T得到的頂點表L；

(4)將r加到表L的末尾，按表L中頂點次序組成迴路H，作為計 算結果返回；

}

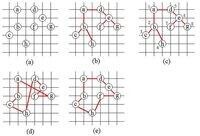
當費用函數滿足三角不等式時，演演算法找出的旅行售貨員迴路的費用不會超過最優旅行售貨員迴路費用的2倍。

(b)表示找到的最小生成樹T；(c)表示對T作前序遍歷的次序；(d)表示L產生的哈密頓迴路H；

(e)是G的一個最小費用旅行售貨員迴路。

在費用 函數不一定滿足三角不等式的一般情況下，不存在具有常數性能比的解TSP問題的多項式時間近似演演算法，除非P=NP。換句話說，若P≠NP，則對任意常數ρ>1，不存在性能比為ρ的解旅行售貨員問題的多項式時間近似演演算法。

問題描述：給定一個完全無向圖G=(V,E)，其每一邊(u,v)∈E有一非負整數費用c(u,v)。要找出G的最小費用哈密頓迴路。

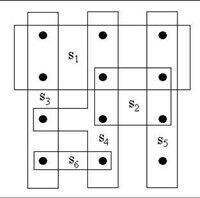
集合復蓋問題的一個實例〈X,F〉由一個有限集X及X的一個子集族F組成。子集族F復蓋了有限集X。也就是說X中每一元素至少屬於F中的一個子集，即X= 。對於F中的一個子集CF，若C中的X的子集復蓋了X，即X= ，則稱C復蓋了X。集合復蓋問題就是要找出F中復蓋X的最小子集C*，使得

|C*|=min{|C||CF且C復蓋X}

集合復蓋問題舉例：

用12個黑點表示集合X。F={S1,S2,S3,S4,S5,S6,}，如圖所示。容易看出，對於這個例子，最小集合復蓋為：C={S3,S4,S5,}。

集合復蓋問題近似演演算法——貪心演演算法

Set greedySetCover (X,F)

{

U=X；

C=；

while (U !=) {

選擇F中使|S∩U|最大的子集S；

U=U-S；

C=C∪{S}；

}

return C；

}

演演算法的循環體最多執行min{|X|，|F|}次。而循環體內的計算顯然可在O(|X||F|)時間內完成。因此，演演算法的計算時間為O(|X||F|min{|X|，|F|})。由此即知，該演演算法是一個多項式時間演演算法。

問題描述：設子集和問題的一個實例為〈S,t〉。其中，S={x1，x2，…，xn}是一個正整數的集合，t是一個正整數。子集和問題判定是否存在S的一個子集S1，使得∑x = t。(x屬於S1)

1 子集和問題的指數時間演演算法

int exactSubsetSum (S,t)

{

int n=|S|；

L={0}；

for (int i=1；i<=n；i++) {

L[i]=mergeLists(L[i-1],L[i-1]+S[i])；

刪去L[i]中超過t的元素；

}

return max(L[n])；

}

演演算法以集合S={x1，x2，…，xn}和目標值t作為輸入。演演算法中用到將2個有序表L1和L2合併成為一個新的有序表的演演算法mergeLists(L1,L2)。

2 子集和問題的完全多項式時間近似格式

基於演演算法exactSubsetSum，通過對錶L[i]作適當的修整建立一個子集和問題的完全多項式時間近似格式。

在對錶L[i]進行修整時，用到一個修整參數δ，0<δ><1。用參數δ修整一個表L是指從L中刪去儘可能多的元素，使得每一個從L中刪去的元素y，都有一個修整后的表L1中的元素z滿足(1-δ)y≤z≤y。可以將z看作是被刪去元素y在修整后的新表L1中的代表。

舉例：若δ=0.1，且L=〈10,11,12,15,20,21,22,23,24,29〉，則用δ對L進行修整后得到L1=〈10，12，15，20，23，29〉。其中被刪去的數11由10來代表，21和22由20來代表，24由23來代表。

對有序表L修整演演算法

List trim(L,δ)

{ int m=|L|；

L1=〈L〉；

int last=L；

for (int i=2；i<=m；i++) {

if (last<(1-δ)*L[i]) {

將L[i]加入表L1的尾部；

last=L[i]；

}

return L1；

}

子集和問題近似格式

int approxSubsetSum(S,t,ε)

{ n=|S|；

L=〈0〉；

for (int i=1；i<=n；i++) {

L[i]=Merge-Lists(L[i-1],

L[i-1]+S[i])；

L[i]=Trim(L[i],ε/n)；

刪去L[i]中超過t的元素；

}

return max(L[n])；

}