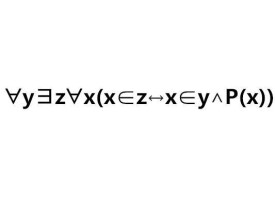子集公理

子集公理的意思是：對於一個已經存在的集合C，可以將其中所有具有性質ψ(x)的元素彙集在一起構成一個新的集合B．顯然，集合B是集合C的子集，子集公理由此得名.

子集公理模式是ZF集合論中公理模式之一，它也叫作分類公理模式、分離公理模式、受限概括公理模式．或簡稱概括公理模式。理解這個公理模式，要注意集合z必須是y的子集。所以，這個公理模式實際上說的是．給定集合y和謂詞P．我們可以找到y的子集z,它的成員完全是滿足P的y的成員。通過外延公理可知．這個集合是唯一的。通常使用集合建造符號把它指示為{x∈y I P(x)}。所以這個公理的本質是：一個集合的通過一個謂詞定義的所有子類自身是一個集合。

無限制的概括公理是說：

∃zᗄx(x∈z↔P(x))。

這個公理表明：存在著一個集合z,它的成員完全是滿足謂詞P的那些對象。集合z再次是唯一的，並通常記為{x丨P(x)}。在採納嚴格公理化之前，這個公理模式默認地用在早年的樸素集合論中。不幸的是，通過採用P(x)為x∉z．它直接導致了羅素悖論。所以，有用的集合論的公理化不使用無限制概括，至少不和經典邏輯公理集合證一起使用。只接受子集公理模式是公理化集合論的開端。多數其他ZF公理系統（不包括外延公理或基礎公理）都包含一個可以替代概括公理的公理；並且．每個這樣公理都聲稱一個特定集合存在，並通過給出它的成員必須滿足的謂詞來定義這個集合。

在貝爾奈斯一哥德爾的集合論中．集合和類之間有著區分。一個類T是集合，當且僅當它屬於某個類y。在這個理淪中，有一個定理模式讀做：

∃xᗄz(z∈x↔(P(x)∧∃y,z∈y)，定義set(x)↔y,x∈y之後，它可以簡寫為

∃xᗄz(z∈x↔(P(x)∧set(z)))。這個公理說明：有一個類x使得任何類z是x的成員，當且僅當z是滿足P的一個集合。這個定理模式自身是受限的概括，避免了羅素悖論，因為它要求z是一個集合。接著把集合自身的分類寫為單一的公理：ᗄxᗄz,set(y)→∃z,set(z)∧ᗄu(u∈z↔u∈y∧u)。

就是說：給定任何類x和任何集合y．有一個集合z,它的成員完全是x和y二者共有的成員。這說明類x和集合y的交集自身是一個集合z。在這個公理中，謂詞P被替代為可量化在其上的類x。

在蒯因( Wilard van Orman Quine)所開創的新基礎集合論中，給定謂詞的概括公理採用無限制形式，但是對可以用於這個模式的謂詞自身是有限制的。謂詞（x∉x）是禁止的，因為同一個符號x出現於成員關係符號的兩端（因而有不同的“相對類型”），從而避免了羅素悖論。但是，採用P（x）為（x=x）是允許的，我們可以形成所有集合的集合。

子集公理和概括原則的聯繫，它們之間的區別在於一個是不加任何限制地將所有具有性質ψ(x)的對象彙集為一個集合，一個是將一個已經存在的集合中具有性質ψ(x)的對象彙集為一個集合．所以，可以認為，子集公理是對概括原則的一個限制。

ZF2空集公理：∃Bᗄx(x∉B).

空集公理的意思是：存在沒有任何元素的集合．

公理集合論ZFC中的公理不具有獨立性，即並非都是不可缺少的．有了子集公理實際上我們可以證明空集公理．因為，根據定理可知，集合是存在的，那麼我們可以任意取定一個集合A，然後使用x≠x作為性質ψ(x)，那麼根據子集公理有：

∃Bᗄx(x∉B↔x∈A∧x≠x),

由此可得:

∃Bᗄx(x∉B).

但是為了方便，人們仍然將空集公理作為公理使用．

一般來說，只有研究的對象存在，這種研究才有意義．

定理1∃x(x=x)．

這是一條邏輯定理．它斷定了集合對象的存在．在公理集合論ZFC的論域中只有集合，除了集合沒有別的研究對象．

定理2 存在一個唯一的集合沒有任何元素．