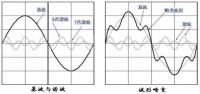
諧波次數

法國數學家傅立葉在1807年就寫成關於熱傳導的基本論文《熱的傳播》，向巴黎科學院呈交，但經拉格朗日、拉普拉斯和勒讓德審閱后被科學院拒絕，1811年又提交了經修改的論文，該文獲科學院大獎，卻未正式發表。傅立葉在論文中推導出著名的熱傳導方程，並在求解該方程時發現解函數可以由三角函數構成的級數形式表示，從而提出任一函數都可以展成三角函數的無窮級數。傅立葉級數（即三角級數）、傅立葉分析等理論均由此創始。

1822年，傅立葉出版了專著《熱的解析理論》（Theorieanalytique de la Chaleur ，Didot ，Paris，1822）。這部經典著作將歐拉、伯努利等人在一些特殊情形下應用的三角級數方法發展成內容豐富的一般理論，三角級數後來就以傅立葉的名字命名。傅立葉應用三角級數求解熱傳導方程，為了處理無窮區域的熱傳導問題又導出了當前所稱的“傅立葉積分”，這一切都極大地推動了偏微分方程邊值問題的研究。然而傅立葉的工作意義遠不止此，它迫使人們對函數概念作修正、推廣，特別是引起了對不連續函數的探討；三角級數收斂性問題更刺激了集合論的誕生。因此，《熱的解析理論》影響了整個19世紀分析嚴格化的進程。傅立葉1822年成為科學院終身秘書。

根據傅立葉級數的原理，周期函數都可以展開為常數與一組具有共同周期的正弦函數和餘弦函數之和。

滿足Dirichlet條件的、以T為周期的時間的周期函數f(t)，在連續點處，可用下述的三角函數的線性組合（傅里葉級數）來表示：

上式稱為f(t)的傅里葉級數，其中，。

n為整數，。

n為整數，。

在間斷點處，下式成立：

為信號f(t)的直流分量。

令

為基波幅值，為n次諧波的幅值。有時也稱一次諧波的幅值。有時也稱0次諧波的幅值。

整數n稱為諧波次數，也稱諧波階數。

諧波的頻率必然也等於基波的頻率的整數倍，基波頻率3倍的波稱之為三次諧波，基波頻率5倍的波稱之為五次諧波，以此類推。不管幾次諧波，他們都是正弦波。

一般來講，變頻器對容量相對較大的電力系統影響不很明顯，而對容量小的系統，諧波產生的干擾就不可忽視，它對公用電網是一種污染。諧波污染對電力系統的危害是嚴重的，主要表現在:

(1)諧波對供電線路產生了附加損耗。由於集膚效應和鄰近效應，使線路電阻隨頻率增加而提高，造成電能的浪費；由於中性線正常時流過電流很小，故其導線較細，當大量的三次諧波流過中性線時，會使導線過熱、絕緣老化、壽命縮短以至損壞;

(2)諧波影響各種電氣設備的正常工作。對如發電機的旋轉電機產生附加功率損耗、發熱、機械振動和雜訊；對斷路器，當電流波形過零點時，由於諧波的存在可能造成高的di/dt,這將使開斷困難，並且延長故障電流的切除時間;

(3)諧波使電網中的電容器產生諧振。工頻下，系統裝設的各種用途的電容器比系統中的感抗要大得多，不會產生諧振，但諧波頻率時，感抗值成倍增加而容抗值成倍減少，這就有可能出現諧振，諧振將放大諧波電流，導致電容器等設備被燒毀;

(4)諧波引起公用電網局部的並聯諧振和串聯諧振，從而使諧波放大，這就使上述危害大大增加，甚至引起嚴重的責任事故;

(5)諧波將使得繼電保護和自動裝置出現誤動作，並使儀錶和電能計量出現較大誤差；諧波對其他系統及電力用戶危害也很大：如對附近的通信系統產生干擾，輕者出現雜訊，降低通信質量，重者丟失信息，使通信系統無法正常工作；影響電子設備工作精度，使精密機械加工的產品質量降低；設備壽命縮短，家用電器工況變壞等.