拓撲動力系統
拓撲動力系統
目錄
設常微分系統
拓撲動力系統
的右側函數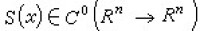 ,且滿足解的惟一性條件,
,且滿足解的惟一性條件,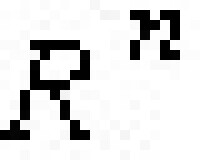 為n維歐幾里得空間。由於S(x)與t無關,不失一般性,可設(*)的每個解φ(x,t)在整個實軸I上有定義,於是它確定了
為n維歐幾里得空間。由於S(x)與t無關,不失一般性,可設(*)的每個解φ(x,t)在整個實軸I上有定義,於是它確定了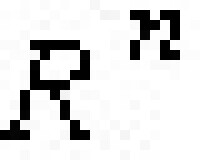 ×I到
×I到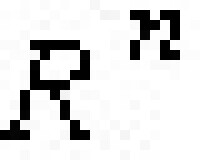 的變換,滿足:
的變換,滿足:
拓撲動力系統
拓撲動力系統
拓撲動力系統
拓撲動力系統
① 初值條件:φ(x,0)=x;
② φ(x,t)對x,t一併連續;
③ 群的條件:即對任意x∈ ,任意t1,t2∈I有
,任意t1,t2∈I有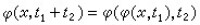 ;
;
拓撲動力系統
拓撲動力系統
④ φ(x,t)對t可微。
為了更一般地研究問題,可以拋開常微分系統,並假設空間是一般的度量空間R。設φ(x,t)是R×I到R且滿足性質①、②、③的單參數連續變換群,則所有這些變換的全體稱為拓撲動力系統或抽象動力系統,記作 ,其中參數t代表時間。點集{φ(x,t),t∈I}稱為過點x的軌線或軌道,記作φ(x,I)。仿此,稱
,其中參數t代表時間。點集{φ(x,t),t∈I}稱為過點x的軌線或軌道,記作φ(x,I)。仿此,稱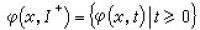 為正半軌線,
為正半軌線,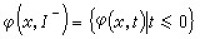 為負半軌線。φ(x;
為負半軌線。φ(x;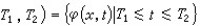 為弧段。當t∈I +(半群),
為弧段。當t∈I +(半群),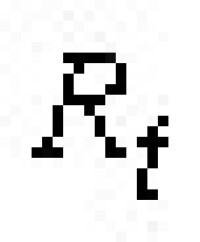 稱為半動力系統或半流;當t∈N(整數加群),
稱為半動力系統或半流;當t∈N(整數加群),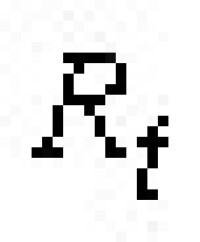 稱為離散動力系統或離散流。若φ(x,t)=x,對一切t∈I,則稱點x為休止點,若φ(x,t+ω)=φ(x,t),對一切t∈I,其中ω>0,則稱φ(x,t)為周期軌線,滿足上述等式的最小正數ω,稱為周期軌線的周期。
稱為離散動力系統或離散流。若φ(x,t)=x,對一切t∈I,則稱點x為休止點,若φ(x,t+ω)=φ(x,t),對一切t∈I,其中ω>0,則稱φ(x,t)為周期軌線,滿足上述等式的最小正數ω,稱為周期軌線的周期。
拓撲動力系統
拓撲動力系統
拓撲動力系統
拓撲動力系統
拓撲動力系統
拓撲動力系統
例如,下面是一個有趣的拓撲動力系統──別布托夫系統。
令勪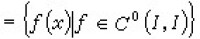 。對於ƒ(x),g(x)∈勪 ,定義距離
。對於ƒ(x),g(x)∈勪 ,定義距離
拓撲動力系統
拓撲動力系統
對距離ρ,勪 構成完備的可分的度量空間。定義映射φ:勪×I→I 如下:
拓撲動力系統
於是它構成一個拓撲動力系統,稱為別布托夫系統,簡記為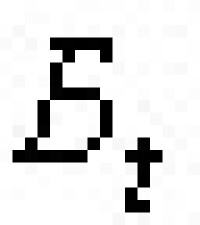 。
。
拓撲動力系統
由n個符號所組成的一切可能的雙無窮序列,在上述類似的距離和軌線的定義下,組成動力系統,稱為符號動力系統,它可視為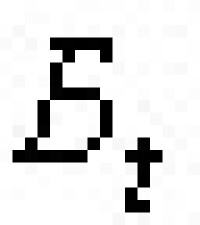 的子系統。很多拓撲動力系統可嵌入
的子系統。很多拓撲動力系統可嵌入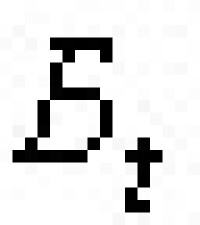 成為它的子系統。
成為它的子系統。
拓撲動力系統
拓撲動力系統
若ƒ(x)呏с,則φ(ƒ(x),t)是休止點;若 ƒ(x+ω)=ƒ(x),對一切x∈I,其中ω>0,則φ(ƒ(x),t)是周期軌線。周期軌線在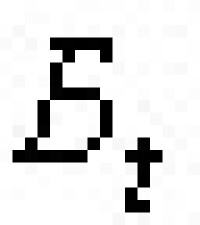 中處處稠密。另外
中處處稠密。另外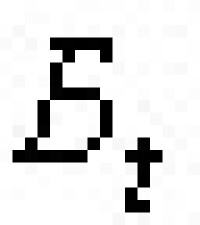 中含有在勪中處處稠密的軌線。
中含有在勪中處處稠密的軌線。
拓撲動力系統
拓撲動力系統
極限點集 設:實數列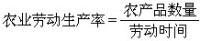 。如果有
。如果有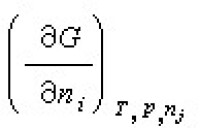 ,則稱點y是軌線 φ(x,t)的ω-極限點,Ωx表示φ(x,t)的一切ω-極限點集。若
,則稱點y是軌線 φ(x,t)的ω-極限點,Ωx表示φ(x,t)的一切ω-極限點集。若 ,則稱y是φ(x, t)的α-極限點,Ax表示φ(x, t)的一切α-極限點集。
,則稱y是φ(x, t)的α-極限點,Ax表示φ(x, t)的一切α-極限點集。
拓撲動力系統
拓撲動力系統
拓撲動力系統
不變集設給定集合A吇R,若對一切t∈I,φ(A,t)=A,則稱A是不變集。Ωx和Ax是閉的不變集。任何一條軌線是不變集,但不一定是閉集。
極小集 集合∑吇R稱為極小集,若它是非空、閉的且不變;同時它沒有任何真子集也具有這三條性質。顯然,Σ中的每一條軌線在Σ上處處稠密。另外,在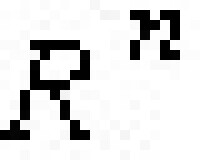 上所定義的拓撲動力系統,若對軌線φ(x,t)而言,
上所定義的拓撲動力系統,若對軌線φ(x,t)而言,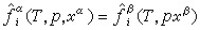 ,則φ(x,I)就是一個極小集,但它不是緊緻的。而比較有趣的是緊緻極小集,如休止點和周期軌線就是緊緻極小集。在R2上定義的連續動力系統的緊緻極小集只能是休止點和周期軌線。但當R≠R2時,情形就不同了。
,則φ(x,I)就是一個極小集,但它不是緊緻的。而比較有趣的是緊緻極小集,如休止點和周期軌線就是緊緻極小集。在R2上定義的連續動力系統的緊緻極小集只能是休止點和周期軌線。但當R≠R2時,情形就不同了。
拓撲動力系統
拓撲動力系統
又如,前例中,當у是無理數時,令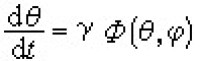 ,
,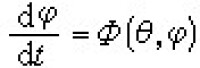 ,式中
,式中  (θ,φ)是對θ,φ周期都為1的連續周期函數。對
(θ,φ)是對θ,φ周期都為1的連續周期函數。對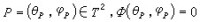 ;當
;當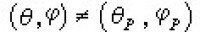 ,
,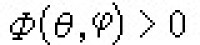 。直觀地說,這就是將前例中的一條過點p且在T2上處處稠密的軌線用奇點p切斷。這時T2不再是極小集,而奇點p是極小集。
。直觀地說,這就是將前例中的一條過點p且在T2上處處稠密的軌線用奇點p切斷。這時T2不再是極小集,而奇點p是極小集。
拓撲動力系統
拓撲動力系統
拓撲動力系統
拓撲動力系統
拓撲動力系統
拓撲動力系統
伯克霍夫證明,若R是緊緻度量空間,則在其上定義的動力系統Rt至少包含一個緊緻極小集。
當R是緊緻的二維定向流形,在其上定義了C2光滑動力系統。若A是Rt的極小集且在R上無處稠密,則A必是休止點或周期軌線。若Ωx中不包含休止點或周期軌線,則Ωx=T2=R。但當Rt只是C1光滑時,A.當儒瓦在1931年舉出過反例(見常微分方程定性理論)。
軌線分類 根據軌線的極限點的性質,可分為:
① 若Ωx=═,則稱φ(x,t)為正向遠離;
② 若Ωx≠═,但φ(x,I)∩Ωx=═,則稱φ(x,t)為正向漸近;
③ 若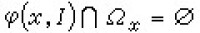 ,則稱φ(x,t)為正向泊松穩定,簡稱p+穩定。
,則稱φ(x,t)為正向泊松穩定,簡稱p+穩定。
拓撲動力系統
仿此,有負向或雙側的遠離、漸近和泊松穩定軌線,後者分別簡稱為p-或p穩定。休止點和周期軌線是p穩定的。R2上的連續動力系統的 p穩定軌線只能是休止點或周期軌線,且其上的 p+或p- 穩定軌線必是p穩定軌線。而當R≠R2時,情形就完全不同了。如前述的T2上被奇點切成兩段的軌線, 一條是p+穩定的, 另一條是p-穩定的,而T2上其餘的都是p 穩定的軌線。比起遠離和漸近軌線來,p 穩定軌線是較複雜和較有興趣的。從天體力學觀點看,p穩定軌線在它的運行過程中,將不斷地在其軌線的任一點的任意小鄰域內再現。與此現象相反的是下面的情形。
設點x∈R,若存在它的鄰域U(x)及時間T>0,使得當t≥T 時,U(x)∩φ(x,t)=═,則稱x為遊盪點。R上的所有遊盪點集W是R上的不變開集。V=R\W是相對於R的非游的點集,它是不變閉集。所有p穩定軌線上的點都是非遊盪點。反之,卻不然。如前述的被奇點切斷的那條軌線,若再用有限個奇點將它切斷,則每兩個奇點之間的那些軌線就既非p-穩定也非p+穩定,但其上都是非遊盪點。
對於p穩定軌線φ(x,t),根據在其運行過程中,它在軌線上任一點的任意小鄰域中再現的時間序列的性質不同,可分成很多類型,除了周期軌線外,最重要的是以下兩類。
若對任給ε>0,存在T(ε)>0及I上對T(ε)而言的相對稠密集{τn},使得對一切t∈I和一切τn,有ρ(φ(x,t),φ(x,t+τn))<ε,則稱軌線φ(x,t)是幾乎周期軌線(或稱概周期軌線)。周期軌線便是幾乎周期的,若周期軌線的周期為ω>0,則可取T(ε)=ω,τn=nω。
若上述相對稠密集{τn}是依賴於軌線上的點y=φ(x,t)或者說依賴於t的,即{τn(t)},則稱φ(x,t)為回復軌線。回復軌線和幾乎周期軌線的閉包的性質是不同的。伯克霍夫證明,緊緻極小集內的每條軌線都是回復的;反之,在完備空間內回復軌線的閉包是緊緻極小集。而緊緻極小集Σ成為幾乎周期軌線的閉包的充分必要條件是:Σ是緊緻、交換、連通拓撲群。
前例中未被奇點切斷的軌線都是p穩定的,但它們不是回復的。類似地,可構造雙周期函數 (θ,φ),使得整個環面T2是回復軌線的閉包而不是幾乎周期軌線的閉包。
(θ,φ),使得整個環面T2是回復軌線的閉包而不是幾乎周期軌線的閉包。
拓撲動力系統
A.M.李亞普諾夫穩定性(見常微分方程運動穩定性理論)、吸引區等概念已經推廣到拓撲動力系統。對非自治微分方程的解來引進動力系統,即所謂“斜積流”,這是值得注意的動向。