梅森素數
專業術語
梅森素數是專業術語,拼音為méi sēn sù shù,是由梅森數而來。
素數是指在大於1的整數中只能被1和其自身整除的數。素數有無窮多個,但到2018年底卻只發現有51個素數能表示成2 -1(p為素數)的形式,這就是梅森素數(如3、7、31、127等等)。它是以17世紀法國數學家馬林·梅森的名字命名。
梅森素數是數論研究中的一項重要內容,自古希臘時代起人們就開始了對梅森素數的探索。由於這種素數具有著獨特的性質(比方說和完全數密切相關)和無窮的魅力,千百年來一直吸引著眾多數學家(包括歐幾里得、費馬、歐拉等)和無數的數學愛好者對它進行探究。
在現代,梅森素數在計算機科學、密碼學等領域有重要的應用價值。它還是人類好奇心、求知慾和榮譽感的最好見證。

梅森素數
1640年6月,費馬在給馬林·梅森(Marin Mersenne)的一封信中寫道:“在艱深的數論研究中,我發現了三個非常重要的性質,我相信它們將成為今後解決素數問題的基礎。”這封信討論了形如2 -1的數。
馬林·梅森是當時歐洲科學界一位獨特的中心人物,他與包括費馬在內的很多科學家經常保持通信聯繫,討論數學、物理等問題。17世紀時,學術刊物和科研機構還沒有創立,交往廣泛、熱情誠摯的梅森就成了歐洲科學家之間聯繫的橋樑,許多科學家都樂於將成果告訴他,然後再由他轉告給更多的人。梅森還是法蘭西學院的奠基人,為科學事業做了很多有益的工作,被選為“100位在世界科學史上有重要地位的科學家”之一。
梅森在歐幾里得、費馬等人有關研究的基礎上對2 -1作了大量的計算、驗證,並於1644年在他的《物理數學隨感》一書中斷言:在不大於257的素數中,當p = 2、3、5、7、13、17、19、31、67、127、257 時,2 -1是素數,其它都是合數。前面的7個數(即2、3、5、7、13、17、19)已被前人所證實,而後面的4個數(即31、67、127、257)則是梅森自己的推斷。由於梅森在科學界有著崇高的學術地位,人們對其斷言都深信不疑。
後來人們才知道梅森的斷言其實包含著若干錯漏。不過他的工作卻極大地激發了人們研究2 -1型素數的熱情,使其擺脫作為“完全數”的附庸地位,可以說梅森的工作是2 -1型素數研究的一個轉折點和里程碑。由於梅森學識淵博、才華橫溢、為人熱情以及最早系統而深入地研究2-1型的數,為了紀念他,數學界就把這種數稱為“梅森數”,並以M記之(其中M為梅森姓名的首字母),即M=2-1。如果梅森數為素數,則稱之為“梅森素數”(即2-1型素數)。
2300多年來,人類僅發現51個梅森素數,由於這種素數珍奇而迷人,因此被人們譽為“數海明珠” 。自梅森提出其斷言后,人們發現的已知最大素數幾乎都是梅森素數,因此尋找新的梅森素數的歷程也就幾乎等同於尋找新的最大素數的歷程。
梅森素數的探尋難度極大,它不僅需要高深的理論和純熟的技巧,而且需要進行艱苦的計算。
在計算能力低下的公元前,人們僅知道四個2 -1型素數:3、7、31和127,發現人已無從考證。15世紀,又一個沒有留下姓名的人在其手稿中給出了第5個2 -1型素數:8191。而在梅森之前,義大利數學家卡達迪(1548~1626)也對這種類型的數進行了整理,他在1588年提出131071和524287也是素數,由此成為第一個在發現者榜單上留名的人。
手算筆錄的時代,每前進一步,都顯得格外艱難。1772年,在卡達迪之後近200年,瑞士數學家歐拉(1707~1783)在雙目失明的情況下,靠心算證明了2147483647是一個素數。這是人們找到的第8個梅森素數,它共有10位數,堪稱當時世界上已知的最大素數。歐拉還證明了歐幾里得關於完全數定理的逆定理:所有的偶完全數都具有2 (2 -1) 的形式,其中2 -1是素數。這表明梅森素數和偶完全數是一一對應的。
梅森素數
梅森素數
梅森素數
1883年,俄國數學家波佛辛(1827~1900)利用盧卡斯定理證明了 也是素數——這是梅森漏掉的。梅森還漏掉另外兩個素數:和,它們分別在1911年和1914年被數學家鮑爾斯(1875~1952)發現。
盧卡斯第一個否定了“M為素數”這一自梅森斷言以來一直被人們相信的結論,但他未能找到其因子。直到1903年,才由數學家科爾(1861~1926)算出M=193707721×761838257287。1922年,數學家克萊契克(1882~1957)進一步驗證了M並不是素數,而是合數。
在手工計算的漫長年代里,人們歷盡艱辛,一共只找到12個梅森素數。
20世紀30年代,美國數學家萊默(1905~1991)改進了盧卡斯的工作,給出了一個針對M的新的素性測試方法,即盧卡斯-萊默檢驗法:M>3是素數當且僅當L=0,其中L=4,L=(L-2)modM。這一方法在“計算機時代”發揮了重要作用。

美國伊利諾伊大學發行的紀念郵戳
梅森素數
梅森素數
梅森素數
1952年,美國數學家魯濱遜(1911~1995)在萊默指導下將此方法編譯成計算機程序,使用SWAC型計算機在幾個月內,就找到了5個梅森素數: 、 、 、和。其後,在1957年被黎塞爾(1929~ 2014)證明是素數;和 在1961年被赫維茲(1937~ )證明是素數。
梅森素數
1963年,美國數學家吉里斯(1928~1975)證明 和 是素數。
1963年6月2日晚上8點,第23個梅森素數 通過大型計算機被找到。發現這一素數的美國伊利諾伊大學數學系全體師生感到無比驕傲,以至於把所有從系裡發出的信件都敲上了“M是個素數”的郵戳。
梅森素數
梅森素數
以IBM360為代表的第三代計算機的出現加快了梅森素數的尋找步伐,但隨著指數p值的增大,每一個梅森素數的產生反而更加艱難。1971年3月4日晚,塔克曼(1915~2002)使用IBM360-91型計算機找到新的梅森素數。而到1978年10月,世界幾乎所有的大新聞機構(包括中國的新華社)都報道了以下消息:兩名年僅18歲的美國高中生諾爾(1960~ )和尼科爾使用Cyber-174型計算機找到了第25個梅森素數。
梅森素數

發現M1257787的Cray-T94型計算機
梅森素數
梅森素數
伴隨數學理論的改善,為尋找梅森素數而使用的計算機也越來越強大,其中包括了著名的超級計算機Cray系列。1979年4月,美國克雷公司計算機專家史洛溫斯基使用Cray-1型計算機找到梅森素數。使用經過改進的Cray-XMP型計算機在1982年至1985年間找到了3個梅森素數: 、和。但他未能確定M和M之間是否有異於M的梅森素數。
梅森素數
1988年,科爾魁特和韋爾什使用NEC-SX2型超高速并行計算機果然發現。沉寂四年之後,哈威爾實驗室(英國原子能技術權威機構)的一個研究小組宣布他們找到梅森素數。
梅森素數
梅森素數
1994年1月10日,史洛溫斯基和蓋奇再次奪回發現已知最大素數的桂冠——這一素數是。而下一個梅森素數 仍是他們的成果,史洛溫斯基由於發現7個梅森素數,而被人們譽為“素數大王” 。1996年發現的M是迄今為止最後一個由超級計算機發現的梅森素數,數學家使用了Cray-T94,這也是人類發現的第34個梅森素數。
使用超級計算機尋找梅森素數實在太昂貴了,而且可以參與的人也有限,網格這一嶄新技術的出現使梅森素數的搜尋又重新回到了“人人參與”的大眾時代。20世紀90年代中後期,在美國程序設計師沃特曼和庫爾沃斯基等人的共同努力下,建立了世界上第一個基於網際網路的分散式計算項目——網際網路梅森素數大搜索(GIMPS)。人們只要在GIMPS的主頁上下載一個計算梅森素數的免費程序,就可以立即參加該項目來搜尋新的梅森素數。
梅森素數
1996年至1998年,GIMPS找到了3個梅森素數: 、和,發現者來自法國、英國和美國。
梅森素數

柯蒂斯·庫珀多次發現“最大素數”
梅森素數
梅森素數
梅森素數
梅森素數
梅森素數
進入21世紀,隨著個人計算機的進一步普及和計算速度的提升,人們又找到不少更大的梅森素數。加拿大青年志願者卡梅倫在2001年11月找到,拉開了新世紀尋找梅森素數的序幕。此後在2003年至2006年間,GIMPS又相繼發現5個梅森素數: 、 、 、和,最大素數紀錄距離1000萬位大關越來越近。
梅森素數
梅森素數
此後一年內,又有兩個1000萬位以上的梅森素數被德國和挪威的志願者先後找出。距史密斯的發現僅相隔兩個星期,而2009年4月找到的 與史密斯發現的素數相比“僅”相差14萬位數。
梅森素數
2013年和2016年,美國中央密蘇里大學數學教授柯蒂斯·庫珀利用校區內的800台電腦連續發現了兩個梅森素數 和。後者其實早在2015年9月就已經被電腦計算出結果,但由於一台協調計算結果的電腦伺服器出了點故障,這一結果直到2016年1月伺服器例行維護時才被發現。庫珀通過GIMPS項目總共發現了四個梅森素數。
梅森素數
2018年4月8日,在發現M超過9年後,該數已被確定為第47個梅森素數。
至2018年12月,總計發現51個梅森素數,並且確定M位於梅森素數序列中的第47位。現把它們的數值、位數、發現時間、發現者等列表如下:
M1~M12
| 序號 | p | 梅森素數 | 位數 | 發現時間 | 發現者 |
梅森素數 | 2 | 3 | 1 | 古代 | 古人 |
梅森素數 | 3 | 7 | 1 | 古代 | 古人 |
| 5 | 31 | 2 | 古代 | 古人 | |
| 7 | 127 | 3 | 古代 | 古人 | |
梅森素數 | 13 | 8191 | 4 | 1456年 | 無名氏 |
梅森素數 | 17 | 131071 | 6 | 1588年 | Pietro Cataldi |
| 19 | 524287 | 6 | 1588年 | Pietro Cataldi | |
梅森素數 | 31 | 2147483647 | 10 | 1772年 | Leonhard Euler |
| 61 | 2305843009213693951 | 19 | 1883年 | Ivan Mikheevich Pervushin | |
| 89 | 618970019642690137449562111 | 27 | 1911年 | Ralph Ernest Powers | |
梅森素數 | 107 | 162259276829213363391578010288127 | 33 | 1914年 | Ralph Ernest Powers |
| 127 | 170141183460469231731687303715884105727 | 39 | 1876年 | Édouard Lucas |
M13~M34
| 序號 | p | 位數 | 發現時間 | 發現者 | 計算機 |
| 521 | 157 | 1952 / 01 / 30 | Raphael MitchelRobinson | SWAC | |
梅森素數 | 607 | 183 | 1952 / 01 / 30 | Raphael MitchelRobinson | SWAC |
| 1,279 | 386 | 1952 / 06 / 25 | Raphael MitchelRobinson | SWAC | |
梅森素數 | 2,203 | 664 | 1952 / 10 / 07 | Raphael MitchelRobinson | SWAC |
梅森素數 | 2,281 | 687 | 1952 / 10 / 09 | Raphael MitchelRobinson | SWAC |
梅森素數 | 3,217 | 969 | 1957 / 09 / 08 | Hans Riesel | BESK |
| 4,253 | 1,281 | 1961 / 11 / 03 | Alexander Hurwitz | IBM 7090 | |
| 4,423 | 1,332 | 1961 / 11 / 03 | Alexander Hurwitz | IBM 7090 | |
梅森素數 | 9,689 | 2,917 | 1963 / 05 / 11 | Donald Bruce Gillies | ILLIAC II |
| 9,941 | 2,993 | 1963 / 05 / 16 | Donald Bruce Gillies | ILLIAC II | |
| 11,213 | 3,376 | 1963 / 06 / 02 | Donald Bruce Gillies | ILLIAC II | |
梅森素數 | 19,937 | 6,002 | 1971 / 03 / 04 | Bryant Tuckerman | IBM 360/91 |
梅森素數 | 21,701 | 6,533 | 1978 / 10 / 30 | Landon Curt Noll &Laura Nickel | CDC Cyber174 |
| 23,209 | 6,987 | 1979 / 02 / 09 | Landon Curt Noll | CDC Cyber174 | |
梅森素數 | 44,497 | 13,395 | 1979 / 04 / 08 | Harry Lewis Nelson & David Slowinski | Cray 1 |
梅森素數 | 86,243 | 25,962 | 1982 / 09 / 25 | David Slowinski | Cray 1 |
| 110,503 | 33,265 | 1988 / 01 / 28 | Walter Colquitt &Luke Welsh | NEC SX-2 | |
| 132,049 | 39,751 | 1983 / 09 / 20 | David Slowinski | Cray X-MP | |
梅森素數 | 216,091 | 65,050 | 1985 / 09 / 06 | David Slowinski | Cray X-MP/24 |
梅森素數 | 756,839 | 227,832 | 1992 / 02 / 19 | David Slowinski &Paul Gage | Harwell Lab's Cray-2 |
| 859,433 | 258,716 | 1994 / 01 / 10 | David Slowinski &Paul Gage | Cray C90 | |
| 1,257,787 | 378,632 | 1996 / 09 / 03 | David Slowinski &Paul Gage | Cray T94 |
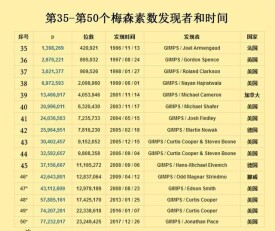
M35~M51
| 序號 | p | 位數 | 發現時間 | 發現者 | 國家 |
| 1,398,269 | 420,921 | 1996 / 11 / 13 | GIMPS / Joel Armengaud | 法國 | |
| 2,976,221 | 895,932 | 1997 / 08 / 24 | GIMPS / Gordon Spence | 英國 | |
| 3,021,377 | 909,526 | 1998 / 01 / 27 | GIMPS / Roland Clarkson | 美國 | |
| 6,972,593 | 2,098,960 | 1999 / 06 / 01 | GIMPS / NayanHajratwala | 美國 | |
| 13,466,917 | 4,053,946 | 2001 / 11 / 14 | GIMPS / MichaelCameron | 加拿大 | |
| 20,996,011 | 6,320,430 | 2003 / 11 / 17 | GIMPS / Michael Shafer | 美國 | |
| 24,036,583 | 7,235,733 | 2004 / 05 / 15 | GIMPS / Josh Findley | 美國 | |
| 25,964,951 | 7,816,230 | 2005 / 02 / 18 | GIMPS / Martin Nowak | 德國 | |
| 30,402,457 | 9,152,052 | 2005 / 12 / 15 | GIMPS / Curtis Cooper & Steven Boone | 美國 | |
| 32,582,657 | 9,808,358 | 2006 / 09 / 04 | GIMPS / Curtis Cooper & Steven Boone | 美國 | |
| 37,156,667 | 11,185,272 | 2008 / 09 / 06 | GIMPS / Hans-MichaelElvenich | 德國 | |
| 42,643,801 | 12,837,064 | 2009 / 04 / 12 | GIMPS / Odd MagnarStrindmo | 挪威 | |
梅森素數 | 43,112,609 | 12,978,189 | 2008 / 08 / 23 | GIMPS / Edson Smith | 美國 |
| 48* | 57,885,161 | 17,425,170 | 2013 / 01 / 25 | GIMPS / Curtis Cooper | 美國 |
| 49* | 74,207,281 | 22,338,618 | 2016 / 01 / 07 | GIMPS / Curtis Cooper | 美國 |
| 50* | 77,232,917 | 23,249,425 | 2017 / 12 / 26 | GIMPS / Jonathan Pace | 美國 |
| 51* | 82,589,933 | 24,862,048 | 2018 / 12 / 07 | GIMPS / Patrick Laroche | 美國 |
註:
1.各表分別列出人工、藉助計算機以及通過GIMPS項目發現的梅森素數。
2.目前還不確定在M47和M51之間是否還存在未知的梅森素數,其後的序號用 * 標出。
3.后兩表梅森素數的數值從略。

EFF向獲獎者(右一)頒發獎金
為了激勵人們尋找梅森素數和促進網格技術發展,總部設在美國舊金山的電子前沿基金會(EFF)於1999年3月向全世界宣布了為通過GIMPS項目來尋找新的更大的梅森素數而設立的獎金。它規定向第一個找到超過100萬位數的個人或機構頒發5萬美元。後面的獎金依次為:超過1000萬位數,10萬美元;超過1億位數,15萬美元;超過10億位數,25萬美元。除此之外,根據EFF關於獎金設立的新規定,任何一位新梅森素數的發現者都將獲得3000美元的研究發現獎。其實絕大多數志願者參與該項目並不是為了金錢,而是出於樂趣、榮譽感和探索精神。
目前人們通過GIMPS項目已找到17個梅森素數,其發現者來自美國(11個)、英國(1個)、法國(1個)、德國(2個)、加拿大(1個)和挪威(1個)。世界上有190多個國家和地區超過60萬人參加了這一國際合作項目,並動用了上百萬台計算機(CPU)聯網來尋找新的梅森素數。該項目的計算能力已超過當今世界上任何一台最先進的超級矢量計算機的計算能力,運算速度達到每秒2300萬億次。著名的《自然》雜誌說:GIMPS項目不僅會進一步激發人們對梅森素數尋找的熱情,而且會引起人們對網格技術應用研究的高度重視。
梅森素數自古以來就是數論研究的一項重要內容,歷史上有不少大數學家都專門研究過這種特殊形式的素數。自古希臘時代起直至17世紀,人們尋找梅森素數的意義似乎只是為了尋找完全數。但自梅森提出其著名斷言后,特別是歐拉證明了歐幾里得關於完全數定理的逆定理以來,偶完全數已僅僅是梅森素數的一種“副產品”了。
尋找梅森素數在當代已有了十分豐富的意義。尋找梅森素數是目前發現已知最大素數的最有效途徑。自歐拉證明M為當時最大的素數以來,在發現已知最大素數的世界性競賽中,梅森素數幾乎囊括了全部冠軍。
尋找梅森素數是測試計算機運算速度及其他功能的有力手段,如M就是1996年9月美國克雷公司在測試其最新超級計算機的運算速度時得到的。梅森素數在推動計算機功能改進方面發揮了獨特作用。發現梅森素數不僅需要高功能的計算機,還需要素數判別和數值計算的理論與方法以及高超巧妙的程序設計技術等等,因此它的研究推動了“數學皇后” ——數論的發展,促進了計算數學和程序設計技術的發展。
尋找梅森素數最新的意義是:它促進了分散式計算技術的發展。從最新的17個梅森素數是在網際網路項目中發現這一事實,可以想象到網路的威力。分散式計算技術使得用大量個人計算機去做本來要用超級計算機才能完成的項目成為可能,這是一個前景非常廣闊的領域。它的探究還推動了快速傅立葉變換的應用。
梅森素數在實用領域也有用武之地,現在人們已將大素數用於現代密碼設計領域。其原理是:將一個很大的數分解成若干素數的乘積非常困難,但將幾個素數相乘卻相對容易得多。在這種密碼設計中,需要使用較大的素數,素數越大,密碼被破譯的可能性就越小。
由於梅森素數的探究需要多種學科和技術的支持,也由於發現新的“大素數”所引起的國際影響,使得對於梅森素數的研究能力已在某種意義上標誌著一個國家的科技水平,而不僅僅是代表數學的研究水平。英國頂尖科學家、牛津大學教授馬科斯·索托伊甚至認為它的研究進展不但是人類智力發展在數學上的一種標誌,同時也是整個科學發展的里程碑之一。
梅森素數這顆數學海洋中的璀璨明珠正以其獨特的魅力,吸引著更多的有志者去尋找和研究。
梅森素數的計算公式
3*5/3.8*7/5.8*11/9.8*13/11.8*......*P/(P-1.2)-1=M
P是梅森數的指數,M是P以下的梅森素數的個數。
以下是計算的數值與實際數的情況:
指數5,計算2.947,實際3 ,誤差0.053;
指數7,計算3.764,實際4 ,誤差 0.236;
指數13,計算4.891,實際5,誤差0.109;
指數17,計算5.339,實際6,誤差0.661;
指數19,計算5.766,實際7,誤差1.234;
指數31,計算6.746,實際8,誤差1.254;
指數61,計算8.445,實際9,誤差0.555;
指數89,計算9.201,實際10,誤差0.799;
指數107,計算9.697,實際11,誤差1.303;
指數127,計算10.036 ,實際12,誤差1.964;
指數521,計算13.818,實際13,誤差-0.818;
指數607,計算14.259,實際14,誤差-0.259;
指數1279,計算16.306,實際15,誤差-1.306;
指數2203,計算17.573,實際16,誤差-1.573;
指數2281,計算17.941,實際17,誤差-0.941;
這個公式是根據梅森素數的分佈規律得出的。萬數1為首,1被除外了,所以要減去1。在不考慮重疊問題,應該P減1就可以了,這裡已考慮重疊問題,所以就P減1.2.在梅森數的指數漸漸增大,1.2是否合適,還要等實際檢驗。
所有的奇素數都是准梅森數(2^N-1)的因 子數,則梅森合數的因子數是只有素數中的一部份。
在2^N-1的數列中,一個素數作為素因子第一次出現在指數N的數中,這個素數作為因子數在2^N-1數列中就以N為周期出現。在這種數列中指數是偶數的都等於3乘以四倍金字塔數。
在2^N-1數列中,指數大於6的,除梅森素數外,都有新增一個或一個以上的素數為因子數,新增的因子數減1能被這個指數整除。
一個梅森合數的因子數只有唯一一次出現在一個梅森合數中。
一個是梅森素數的素數,它永遠不是梅森合數的因子數。
一個是前面的梅森合數的因子數的素數,它永遠不會是後面的梅森合數的因子數。
所有梅森合數的因子數減1都能被這個梅森合數的指數整除,商是偶數。
一個素數在不是梅森合數的准梅森數中第一次以因子數出現,這個素數減1能被這個准梅森數的指數整除,商不一定是偶數。
梅森素數都在[4^(1-1)+4^(2-1)+4^(3-1)+......+4^(n-1)]*6+1數列中,括符里種數暫叫四倍金字塔數。
凡是一個素數是四倍金字塔數的因子數,以後就不是梅森合數的因子數。
在4^(1-1)+4^(2-1)+4^(3-1)+......+4^(n-1)數列中的數,有不等於6NM+-(N+M)的數乘以6加上1都是梅森素數。
在2^P-1平方根以下的素數都以素因子在以前准梅森數中出現了,那這個梅森數必是梅森素數。但它的逆定理是不成立的。如果還沒有出現在以前的准梅森數中的素數,它也不定是梅森合數的因子數。
梅森合數的因子數都是8N+1和8N-1形的素數。
試證梅森素數
在指數n是無限多的2^n-1數列中梅森數和梅森素數只佔其中的很少比例。
根據費馬小定理,每一個奇素數都會以數因子出現在2^n-1數列中,只不過有些提前出現,有些最後出現。只有梅森素數是最早出現在這個數列中的。其他有素數都不會最早出現,最遲出現的素數是在本數減1的數中,也就是費馬小定理的地方。
每一個奇素數都十分有規律作為因子數出現在2^n-1數列中,一個素數第一次出現在2^n-1數中(包括梅森素數),這個素數就以n為周期反覆出現在2^n-1數列中,如3第一次出現在n=2中,指數能被2整除的都有3的因子數;7第一次出現在n=3,指數能被3整除的都有7的因子數;5第一次出現在n=4中,指數能被4整除都有5的因子數。一個素數出現在2^n-1數列n中,不管n是素數不是素數,只要用小於n的全部奇素數去篩,指數n都在其中。如果是合數與前面的素數是重疊的,所以不用重篩了。
要篩完2^n-1數列中所有數因子,必需用少於或等於2^n-1平方根以內的所有素數去篩,這樣剩下沒有篩的就是梅森素數了。
2^n-1的數列是無限多的,無限多的自然數任你篩多少次的幾分之一,永遠是無限多的。所以梅森素數是無限多的。
梅森素數的篩法
根據費馬小定理,每一個奇素數都會以素因子的身份出現在2^n-1數列中,只不過有些出現早,有些出現遲。
每一個奇素數第一次出現在2^n-1數列指數n的數中,這個n就是這個素數的對應數,它就以n為周期反覆出現。
已經知道梅森素數都出現在梅森數中。只要篩去梅森數中的梅森合數,剩下就是梅森素數。
將梅森數列展開,從3的對應數2開始,2點一點;5的對應數是4,4是合數,就不用操作;7的對應數是3,在3點一點;11的對應數是10,是合數,不用操作;13的對應數是12,12是合數,不用操作;這樣一直點下去,點到梅森數的指數以前的數都能篩凈。凡是一個梅森數點上兩次和兩次以上的都給劃去,剩下就是只有點一次的梅森數了,這些梅森數全是梅森素數。
這個篩法在素數很大時找它的對應數有點困難。