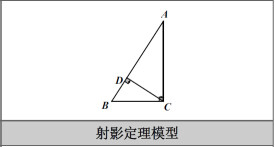
射影定律
數學家歐幾里得提出的幾何定理
射影定理,又稱“歐幾里德定理”,定理內容是直角三角形中,斜邊上的高是兩直角邊在斜邊上射影的比例中項,每一條直角邊是這條直角邊在斜邊上的射影和斜邊的比例中項。公式表達為:如左圖,在Rt△ABC中,∠ACB=90°,cd是斜邊ab上的高,則有射影定理如下:①CD²=AD·DB,②BC²=BD·BA, ③AC²=AD·AB; ④AC·BC=AB·CD(等積式,可用面積來證明)。
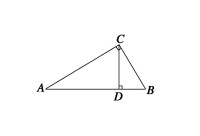
射影定律簡圖(幾何畫板)
設直角三角形ABC,AB是斜邊,CD是高,則AC的平方=AD×AB
CB的平方=BD×BACD的平方=AD×DB等積式;
AD×AC=AB×AC
推出;AC/AB=AD/AC(比例式)
如圖,∠ABC=90°,CD⊥AB,則AC^2=AD×AB,BC^2=BD×AB,CD^2=AD×BD。以上比例式合稱射影定理。主要用於解決直角三角形斜邊及定點與斜邊的連線的問題,比如說給出AD和BD的長度求AC:BC。
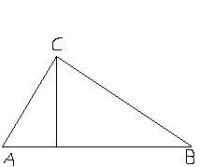
射影定律
其中,從一點到一條直線所作垂線的垂足,叫做這點在這條直線上的正投影。一條線段的兩個端點在一條直線上的正投影之間的線段,叫做這條線段在這直線上的正投影。
公式: 如圖,Rt△ABC中,∠ABC=90°,BD是斜邊AC上的高,則有射影定理如下:
(1)(BD)^2=AD·DC, (2)(AB)^2=AD·AC , (3)(BC)^2=CD·CA 。
等積式(4)AB×BC=AC×BD(可用“面積法”來證明)
射影定理簡圖(幾何畫板)
:(主要是從三角形的相似比推算來的)一、
在△BAD與△BCD中,∵∠ABD+∠CBD=90°,且∠CBD+∠C=90°,
∴∠ABD=∠C,
又∵∠BDA=∠BDC=90°
∴△BAD∽△CBD
∴ AD/BD=BD/CD
即BD^2=AD·DC。其餘同理可得可證
註:由上述射影定理還可以證明勾股定理。
有射影定理如下:
AB^2=AD·AC,BC^2=CD·CA
兩式相加得:
AB^2+BC^2=AD·AC+CD·AC =(AD+CD)·AC=AC^2 .
即AB^2+BC^2=AC^2(勾股定理結論)。
二、
已知:三角形中角A=90度,AD是高.
用勾股證射影
∵AD^2=AB^2-BD^2=AC^2-CD^2,
∴2AD^2=AB+AC-BD-CD=BC-BD-CD=(BD+CD)-(BD+CD)=2BD×CD.
故AD^2=BD×CD.
運用此結論可得:AB=BD+AD=BD+BD×CD=BD×(BD+CD) =BD×BC, AC=CD+AD=CD+BD×CD=CD(BD+CD)=CD×CB.
綜上所述得到射影定理。同樣也可以利用三角形面積知識進行證明。
任意三角形射影定理又稱“第一餘弦定理” :
△ABC的三邊是a、b、c,它們所對的角分別是A、B、C,則有
a=b·cosC+c·cosB,
b=c·cosA+a·cosC,
c=a·cosB+b·cosA。
註:以“a=b·cosC+c·cosB”為例,b、c在a上的射影分別為b·cosC、c·cosB,故名射影定理。
證明1:設點A在直線BC上的射影為點D,則AB、AC在直線BC上的射影分別為BD、CD,且
BD=c·cosB,CD=b·cosC,∴a=BD+CD=b·cosC+c·cosB. 同理可證其餘。
=acosB+(asinB/sinA)cosA=a·cosB+b·cosA. 同理可證其它的。
面積射影定理:“平面圖形射影面積等於被射影圖形的面積S乘以該圖形所在平面與射影面所夾角的餘弦。”
COSθ=S射影/S原
(平面多邊形及其射影的面積分別是S原,S射影,它們所在平面所成銳二面角的為θ)
因為射影就是將原圖形的長度(三角形中稱高)縮放,所以寬度是不變的,又因為平面多邊形的面積比=邊長的平方比。所以就是圖形的長度(三角形中稱高)的比。那麼這個比值應該是平面所成角的餘弦值。在兩平面中作一直角三角形,並使斜邊和一直角邊垂直於棱(即原多邊形圖的平面和射影平面的交線),那麼三角形的斜邊和另一直角邊就是其多邊形的長度比,即為平面多邊形的面積比,而將這個比值放到該平面三角形中去運算即可。