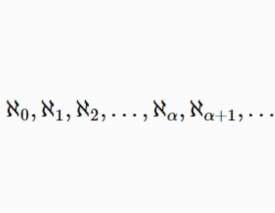後繼基數

後繼基數是一種不可數基數 ，在超限基數正則序列中，稱為的 後繼基數，稱為 的前行基數。一個基數與它的後繼基數是緊相鄰的兩個基數，即不存在基數，使成立，每一基數都有後繼基數，但極限基數與 沒有前行基數，在廣義連續統假設下，的後繼基數。

極限基數是一種不可數基數，即與後繼基數相對的一類基數。在超限基數正則序列中，若序數α是極限序數，則稱為極限基數。每一個超限基數都是極限序數，若是一極限序數，則是序列 的極限。

超限基數亦稱無限基數，是一類常見的基數，指與有限基數相對的一類基數，可數基數、不可數基數統稱超限基數，超限基數又稱為阿列夫()，將所有超限基數從小到大排列出來，得到正則超限基數序列： ，是一個無限上升的良序鏈，這裡是可數基數，也是最小的超限基數，當時，都是不可數基數。

超限基數有下列性質：

1.對任何基數a，都存在比它更大的基數b，即；

2.若，則是一個基數；

3.超限基數等冪定理：對任何序數α，

4.對任何序數α與β，

5.對任何序數α與β，當時，

6.對任何序數α，

不可數基數是一種無窮基數，不可數集的基數統稱為不可數基數。一個無窮集合，如果不與自然數集等勢，它就具有不可數基數。例如實數集R的基數、R的冪集的基數都是不可數基數。不可數基數有無窮多個等級。因為根據著名的康托爾定理：對任何基數，故可得