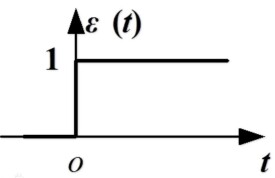
階躍函數

在數學中，如果實數域上的某個函數可以用半開區間上的指示函數的有限次線性組合來表示，那麼這個函數就是階躍函數。階躍函數是有限段分段常數函數的組合。

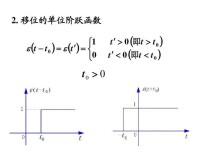
階躍函數是奇異函數，時，函數值為0；時，函數值為1/2,；時，函數值為1

。

按廣義函數理論，單位階躍函數ε(t)的定義為：

即階躍函數ε(t)作用與檢驗函數φ(t)的效果是賦予它一個數值，該值等於φ(t)在(0,∞)區間的定積分

。

通過階躍信號來表示複雜的信號，可以簡化對複雜信號的一些特性的研究。階躍信號及其延時階躍信號的線性組合來表示或逼近，再利用系統的迭加原理，可以通過簡單的信號如單位階躍信號的頻譜，以及頻域特性來討論比較複雜信號的頻譜。從而減少計算複雜信號頻譜的難度。

在作積分變換時，對於分段定義的原函數和像函數必須分段處理，常常很麻煩而且容易出錯。利用階躍函數可將分段定義的函數表示成統一的形式，將函數切割或將分段定義的函數統一地表示成定義在整個數軸上的函數，常使變換簡捷容易，簡化運算，減少錯誤。

（1）可以方便地表示某些信號；

（2）用階躍函數表示信號的作用區間；

（3）階躍函數的拉氏變換為：。

單位衝激函數等於單位階躍函數對時間變數的導數：

反之，單位階躍函數等於單位衝激函數的積分：

階躍響應g(t)定義為：系統在單位階躍信號u(t)的激勵下產生的零狀態響應。即激勵所發出的信號為階躍函數，產生了零狀態響應（電路的儲能元器件（電容、電感類元件）無初始儲能，僅由外部激勵作用而產生的響應。）

自然生態

利用階躍函數提出數學模型解決自然生態問題。例如《基於階躍函數的紅樹林凋落物變化模型研究》：由於凋落物隨時間變化而存在峰值,利用階躍函數,解決了分段模型一直無法解決的兩個問題:一是變點的數學確定方法,另一個是變點的連續性問題。建立了基於符號函數的階躍函數模型,並以此為基礎,提出了具有峰值的凋落物耦合模型。

高精度逼近

改進了階躍函數及其反函數的近似逼近函數——磨光函數和過濾函數，以提高ICM(Independent Continuous and Mapping,即獨立、連續及映射)方法求解結構拓撲優化問題的效率。

工程領域

如通過延遲階躍函數求解重複性項目控制路線的方法研究、橋樑氣動導納識別的階躍函數擬合法、用多項式和階躍函數構造網格多渦卷混沌吸引子及其電路實現等等都有不同程度上的發現。