五邊形

德國數學家卡爾·萊因哈特於1918年發現了五種可以鑲嵌平面的五邊形，從那時起，尋找可以鑲嵌平面的五邊形並將它們分類就成為了一個數學世紀難題。

很多人都認為萊因哈特已經把所有可以鑲嵌平面的五邊形都找出來了，但事實並非如此：1968年，R·B·克什納又發現了三種；1975年，理查德·詹姆斯將紀錄刷新到了9種；同年，聖地亞哥一位50多歲的家庭主婦馬喬里·賴斯。從《科學美國人》雜誌中獲知了詹姆斯的發現，作為一名業餘數學家，賴斯發明了自己的數學符號和方法，並在接下來的幾年內發現了另外四種可以鑲嵌的五邊形。

1985年，羅爾夫·施泰因發現了第14種。似乎這樣的五邊形還會越來越多。不過，在那之後五邊形追蹤行動似乎陷入了低谷。

2015年8月19日，美國華盛頓大學研究團隊發現了一種新的不規則五邊形，相互組合后可完全鋪滿平面，不會出現重迭或有任何空隙，是全球第15種能做到此效果的五邊形。而距上次發現類似效果的五邊形已時隔30年，這項發現相當於在數學領域中尋了獲新原子粒子。

邊長為a的正五邊形，其面積就是:

540度。

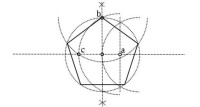
約前300年，歐幾里得在他的《幾何原本》中描述了一個用直尺和圓規做出正五邊形的過程。

1.畫一條水平線，通過此線上的任意點做一個圓。

2.將圓規的一腿放在圓與直線的其一交點上，通過上述圓的圓心畫半圓，並與之交兩點。連接這兩點做垂直線，與先前的水平線相交與(a)點.

3.張開圓規，以水平線與第一個圓的兩個交點為圓心以相同半徑在水平線上下第一個圓外分別做兩個交點，這樣可以得到一條通過第一個圓圓心的正交線，與第一個圓相交的位於水平線上方的點稱之為(b).這是正五邊形的第一個角。

4.將圓規的一腳放在(a)點上，(a)(b)間距為半徑做另一個圓，交水平線於點(c)。

5.將圓規的一腳放在(b)點上，(b)(c)間距為半徑做圓，交第一個圓於兩點，這是正五邊形的第二、三兩點。

6.將圓規的一腳分別放在二、三兩點上，同樣是(b)(c)間距為半徑交第一個圓於另外兩點，這兩點就是正五邊形的最後兩點。

7.連接相鄰兩點就構成了正五邊形。

8.如果不是連接相鄰兩點（即對角線連接），就會得到一個五角星，在它的中間構成一個小的正五邊形。或者延長每一邊，得到一個大的正五角星。

正五邊形五邊相等，五個內角相等，都是108°

正五邊形的五條對角線都相等

正五邊形是軸對稱圖形，共有5條對稱軸。

正五邊形的每個外角和每個中心角都是72°

正五邊形不是中心對稱圖形

正五邊形有一個外接圓和一個內切圓

正五邊形是旋轉對稱圖形，旋轉中心就是正五邊形的中心。