平面流動
平面流動
平面流動(plane flow)是一類特殊流動。如果各點的流速都平行於某一平面,並且所有物理量在此平面的垂直方向上是不變的,則稱此流動是平面流動。對平面流動,總可以找到某直角坐標系Oxyz,在此坐標系中,沿z軸的速度分量為零,並且所有物理量對z的偏導數均為零。
平面流動基本上是一種理想流動,湍流無例外是三維的,研究平面流動流動是流體之間、流體與固體之間的相對滑過,流體運動的軌跡很容易就變成曲折的、渦旋形態的,許多流動顯示實驗表明湍流渦旋演化(卷吸、摻混等)將造成流體的裂解、重組,使得流體的連續性在一定程度上被破壞了,流動的Lagrangian描述面臨奇異性的挑戰:要保證可以跟蹤標示的流體質點概念的有效性,有限大(數值計算)模型必須可以逼近無限小(數學物理)模型,現在湍流破壞了這種連接。同時,起初改變流體輸運進程的單純的大尺度渦旋結構也變成多尺度、嵌套的渦旋結構,並且渦旋結構不再只是流體輸運特徵的表徵,也可能成為被輸運的對象,小尺度渦旋具有獨立於主流和邊界條件的普適特徵就是這種轉變的一個反映。另一方面,雖然小尺度渦旋應該在所有尺度上均表現為小尺度,但所謂的大尺度渦旋卻並非在所有方向上都呈現為大尺度,比如在混合層、射流卷吸過程中形成的大尺度渦旋就包含薄剪切層結構、新近在旋轉流中觀察到的絲狀結構則只有一個方向上呈現為大尺度。
對靜止流體,無論是氣體還是液體,流體(微粒)在分了熱運動過程中不僅有平移還有旋轉,流體單元,宏定向(速度場奇性),微定向(輸運奇性),微渦旋理論上,流體粘性力表述的客觀性要求必然導致渦旋場的引入;現象上,湍流速度信號的層次結構特徵也有必要引入新的序參量加以描述。為此,鄒文楠等借鑒規範場理論一些原理並通過廣義流的分析得到流體拉氏量密度的表示,建立了包含壓力場、速度場和渦旋場的新型流體動力學系統,其中渦旋場描述了統計平均的白組織的微(渦旋)運動和微(錯位)結構。與速度場不同,渦旋場展現的渦旋結構則是嵌套的、隨機的一一在一個連續變化的尺度上統計平均地存在的渦旋。渦旋場描述的微渦旋及其描述的微結構誘導速度場方向畸變的效應還可以看作是對微觀擴散(和/或粘附)的內涵的擴充,即在平衡擴散的基礎上加入的自組織有序擴散的描述,從而大大豐富了流體粘性作用的機理,並且實際上建立了遠離平衡態流動中粘性耗散結構的描述。

平面流動
平面流動
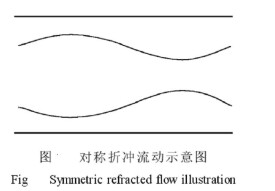
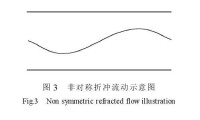
在實驗中,可以經常觀測到對稱邊界明渠突擴流動存在不止一個平面對稱解,如圖1、圖2所示。也經常觀測到 下游不對稱蟻亦即非對稱折衝流動),如圖3所示。這種非對稱折衝流動可能與上游突擴前斷面非對稱入口條件相對應,也可能與上游突擴前斷面對稱入口條件相對應。對稱邊界圓管突擴流動可能存在不止一個軸對稱解,當突擴前入口斷面給定均勻流速分佈或最大流速在軸線流速分佈狀態時,突擴之後下游斷面也可能存在最大流速不在軸線的軸對稱解。Dust,F等通過試驗發現當時(u是突擴噴口的最大流速,H是噴口寬度,v是粘性係數),突擴后的流動是對稱的;時,流動突擴后的流動偏向一側,即最大流速不在軸線;當時,又偏向另一側。槐文信、李煒在其論文中通過數值計算的方法也證實了Dust,F等人的試驗結果。這表明突擴后的流動形態取決於雷諾數Re。對稱邊界條件下存在多解性問題。推而廣之,非對稱邊界條件下也應該存在多解性問題。對實際工程問題,所關心的解的特徵值是與確定的解相對應的。最終作為控制條件的解的特徵值必須在所有的解數中搜索。所以,對流動多解性問題的討論與分析,無論從理論還是實際工程應用方面都具有重要的意義。
李占松等從定常二維平面流動的流函數渦量型方程出發, 從理論上推導出一種不同於通常提法的二維平面流動的定解提法。為解決此類流動的多解性問題奠定了理論基礎。同時,討論了明渠突擴流動和圓管突擴流動中存在的不止一個對稱解問題,並就此問題未被重視的原因進行了初步分析。