圓內接四邊形
一個幾何概念
圓內接四邊形(Cyclic quadrilateral)是一個幾何概念,是指四個頂點均在同一圓上的四邊形。圓內接四邊形擁有很多幾何性質,可用於數學幾何問題求解。
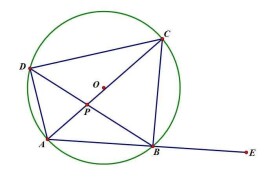
以右圖所示圓內接四邊形ABCD為例,圓心為O,延長AB至E,AC、BD交於P,則:
1.圓內接四邊形的對角互補:
2.圓內接四邊形的任意一個外角等於它的內對角:
3.圓心角的度數等於所對弧的圓周角的度數的兩倍:
4.同弧所對的圓周角相等:
5.圓內接四邊形對應三角形相似:(三個內角對應相等)
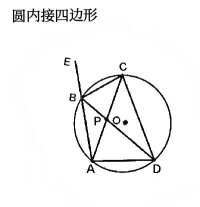
示例圖
7.托勒密定理:
1、如果一個四邊形的對角互補,那麼這個四邊形內接於一個圓;
2、如果一個四邊形的外角等於它的內對角,那麼這個四邊形內接於一個圓;
3、如果一個四邊形的四個頂點與某定點等距離,那麼這個四邊形內接於以該點為圓心的一個圓;
4、若有兩個同底的三角形,另一頂點都在底的同旁,且頂角相等,那麼這兩個三角形有公共的外接圓;
5、如果一個四邊形的張角相等,那麼這個四邊形內接於一個圓;
7、托勒密定理的逆定理。
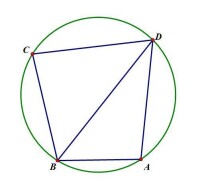
例題1
在圓內接四邊形ABCD中,,則BC的長為_______?
答案
使用餘弦定理:,解得,
因為:圓內接四邊形對角互補,
所以:
使用正弦定理:
即
所以:
例題2:
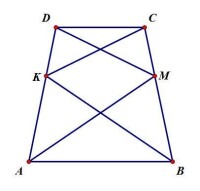
例題2(題圖)
求證:(第二屆袓沖之杯初中數學競賽考題)
答案
證明:聯結KM與BC延長線上一點E。
因為:
所以:AKMB四點共圓
因為:
所以:
所以:
所以:CDKM四點共圓
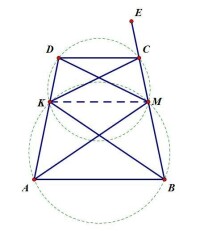
例題2(答案圖)
所以: