GWR

在空間分析中，觀測數據一般按照給定的地理位置作為採樣單元進行採樣，隨著地理位置的變化，變數間的關係或者結構會發生改變，即GIS中所說的“空間非平穩性”。這種空間非平穩性普遍存在於空間數據中，如不同省份的AIDS發病率、湖泊不同深度TN含量、城市工業區與非工業區PM2.5濃度等等。如果採用傳統的線性回歸模型來分析空間數據，一般很難得到令人滿意的結果，因為全局模型在分析前就假定了變數間的關係具有“各向同性”，所得結果只是研究區域內的某種“平均”。因此，有必要採用一種新的局部回歸方法，來應對空間數據自身的這種屬性。GWR模型便順勢被研究者提出並加以大量實踐和驗證。

在傳統回歸分析中，如最小二乘模型（OLS），基本假設是自變數與因變數的關係在整個地區保持穩定。常見形式為：

OLS模型作為一種全局回歸模型，其得到的回歸係數估計值是整個研究區域內的平均值，不能反應回歸參數的真實空間特徵。為了解決這一問題，國外有些學者提出了空間變參數回歸模型（Foster et al.,1986），全局模型中的參數是地理位置的某種函數，從而參數在空間中的變化趨勢就得以度量。Fortheringham et al.(1996)在總結局部回歸分析和變參數研究的基礎上，借鑒局部平滑滑思想，提出了地理加權回歸模型（GWR）。

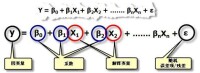
地理加權回歸是對普通線性回歸模型的擴展，將數據的空間位置嵌入到回歸方程中，形式如下：

上式中，為採樣點i 坐標，為採樣點i上的第k個回歸參數，是關於地理位置的函數，在估算的過程中採用權函數的方法得到。

GWR模型的核心是空間權重矩陣，其選取的適當與否對回歸參數的正確估計至關重要，比較常見的空間權函數有：1.距離閾值法；2.距離反比法；3.Gauss函數法等，各自對應的具體形式如下：

距離閾值法是自檢單的權函數選取方法，其關鍵是選取合適的距離閾值D與d進行對比，若大於閾值則權重為0，否則為1，形式如下：

假定空間相近的地物比較遠的地物具有更強的相關性，基本形式為：

基本思想是通過選取一個連續單調遞減函數表示權重與距離之間的關係，以此來克服以上兩種方法的缺點。滿足要求的函數有多個，Gauss函數因其普適性而得到廣泛應用，函數形式如下：

式中b是描述權重與距離之間函數關係的非負數衰減參數，稱為帶寬。帶寬越大，權重隨距離增加衰減得越慢，反之則權重衰減得越快。

當前GWR模型已被應用到經濟、自然資源管理、醫學多個等研究領域。