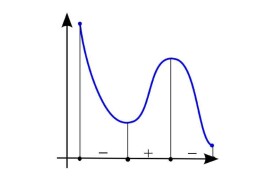
單調區間
專業術語
單調區間,專業術語,拼音為dān diào qū jiān,是指函數在某一區間內的函數值y隨自變數x的值增大而增大(或減小)恆成立。若函數y=f(x)在某個區間是增函數或減函數,則說明函數在這一區間具有(嚴格的)單調性,這一區間叫做函數的單調區間。此時也說明函數是這一區間上的單調函數。
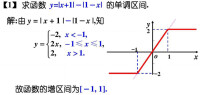
單調區間
註:在單調性中有如下性質。圖例:↑(增函數)↓(減函數)
↑+↑=↑ 兩個增函數之和仍為增函數
↑-↓=↑ 增函數減去減函數為增函數
↓+↓=↓ 兩個減函數之和仍為減函數
↓-↑=↓ 減函數減去增函數為減函數
一般地,設函數f(x)的定義域為I:
如果對於屬於I內某個區間上的任意兩個自變數的值x1、x2,當x1增函數。
相反地,如果對於屬於I內某個區間上的任意兩個自變數的值x1、x2,當x1f(x2),那麼f(x)在這個區間上是減函數。
y=√(X²+2X—3)