本原多項式
近世代數中的概念
一個n次不可約多項式,如果只能整除1+Z^2^n-1
而不能整除其它1-Z^L(L<2^n-1),則這種不可約多項式就稱為本原多項式。
本原多項式的另外一種定義:係數取自GF(p)上,以GF(p^m)上的本原域元素為根的最小多項式。
因為本原多項式一定以n=p^m-1級元素為根,p^m≡1(mod n),所以本原多項式的次數必然是m。
對於一個n次多項式,其本原多項式一般有若干個。下面將給出的一個演演算法,是求解在給定任意n值及一個本原多項式的情況下,其餘本原多項式的求解方法。該演演算法的意義在於提供了同一n值情況下若干個可選的本原多項式,這樣就允許在構造應用系統時有不同的選擇方案。
已知一個n級本原多項式,求解其餘的本原多項式按以下步驟進行。
(1) 首先確定n級本原多項式的個數λ(n),λ(n)即是n級本原多項式的個數。
(2) 求出小於2n-1且與2n-1互素的所有正整數,構成一個集合〔Si〕,並重新排序,使〔Si〕中元素從小到大排列。
(3) 排除〔Si〕中不適合的數
* 排除〔Si〕中形如2j(j為正整數)
* 排除〔Si〕中所有同宗的數。即從〔Si〕中從後到前搜索,每取一個數即做2K×Si,直到大於2n-1,然後減去2n-1,用差值在〔Si〕中向前搜索,如果有相同的數則將Si排除,否則保留。再取Si-1按同樣過程做一遍,直到S0.
* 排除〔Si〕中有倍數關係的數。即從〔Si〕中從後到前搜索,每取一數即向前查詢一遍,最後〔Si〕中剩下的數即為本原抽樣數,其個數一定為λ(n)-1。
(4) 根據已知的一個n級本原多項式,為其設置初始狀態000…01(n個),求出其M序列{Ai}(長度為2n-1).
(5) 依次從Si中取出本原抽樣數,每取出一個抽樣數Si,即可求出一個本原多項式:以Si對{Ai}進行抽樣,就可產生長度為2n-1的另一M序列{Si},在{Si}中找到形如000…01(n位)的序列段{Mi},並提取包括{Mi}為前n項的2n長度的序列:
Am+0,Am+1,…,Am+n-1,
0 0 … 1
Am+n,Am+n+1,…Am+2n-1
X X … X
欲確定的Ci可用下列方程組確定;
C1=Am+n
C2=Am+n+1+C1Am+n
C3=Am+n+2+C1Am+n+1+C2Am+n
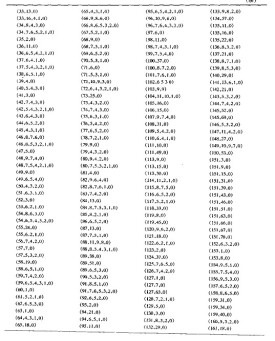
下表為常用本原多項式:
Matlab中調用本原多項式的指令:
primpoly(m);
primpoly(m,'all');
primpoly(m,'all','nodisplay');

本原多項式