瑞利-金斯公式
瑞利-金斯公式
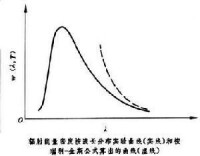
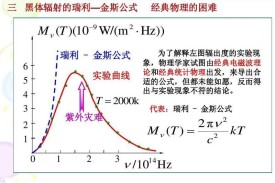
瑞利-金斯公式,是根據經典電動力學和統計力學導出的熱平衡輻射能量分佈公式。瑞利(1900)和金斯,J.H.(1905)根據經典統計理論,研究密封空腔中的電磁場,得到了空腔輻射的能量密度w(v,T)按頻率v分佈的瑞利-金斯公式
瑞利和金斯求出在頻率間隔內本徵振動的個數為
其中因子2是由於每一頻率v對應於偏振面互相垂直的兩個波的緣故。
根據經典能量均分定理,每個振動自由度的平均能量為kT,即的平均動能和的平均勢能,
所以將式(2)乘以kT,並用體積V除,就得到頻率之間、單位體積的能量表示式,即式(1)。
也可將式(1)換為按波長的分佈公式。