控制理論

控制理論的發展歷史可分為兩個階段經典控制理論與現代控制理論。

經典控制理論即古典控制理論，也稱為自動控制理論。

20世紀初研製成裝在飛機上的電動陀螺穩定裝置，並發展成自動駕駛儀，但這僅僅是人們在實踐中直觀摸索的結果，尚無理論上的指導。當時的自動駕駛儀在結構上比較簡陋，對飛機的穩定和控制也極為簡單，控制質量不高。30年代末至40年代初形成經典控制理論。在這種理論指導下飛機上自動駕駛儀的性能得到提高，並在40年代為研製V-1、V-2導彈提供了基礎。經典控制理論適用於單輸入、單輸出的線性定常（參數不隨時間而變）系統，所以在分析設計V-1、V-2導彈控制系統時，將導彈的運動分解成單輸入、單輸出的運動。V-2導彈從地面飛出大氣層，其特性參數變化很大，是一個時變對象，但為了應用經典控制理論而採用係數凍結法將時變對象簡化為定常的對象。這樣，V-1和V-2導彈雖都投入使用，但命中精度不高。經典控制理論中的非線性理論在40～50年代得到發展，經典的分析方法有描述函數法、相平面法等。這些分析方法在分析戰術導彈制導系統（較多採用典型非線性的繼電控制方式）時較為有效，成為50年代戰術導彈得到較大發展的因素之一。

隨著導彈和航天活動的進展，對飛行器控制的精度要求大大提高，飛行器完成的任務更趨複雜，加上飛行器飛行時環境的急劇變化，對飛行器控制系統提出了更高的要求。為了滿足這些要求，必須尋求新的理論來指導控制系統的設計。

經典控制理論的發展歷程

1.萌芽階段

早在古代，勞動人民就憑藉生產實踐中積累的豐富經驗和對反饋概念的直觀認識，發明了許多閃爍控制理論智慧火花的傑作。如果要追溯自動控制技術的發展歷史早在兩千年前中國就有了自動控制技術的萌芽。例如，兩千年前我國發明的指南車，就是一種開環自動調節系統。它利用差速齒輪原理，利用齒輪傳動系統，根據車輪的轉動，由車上木人指示方向。不論車子轉向何方，木人的手始終指向南方，“車雖回運而手常指南”。

我國北宋時代（公元1086～1089年）蘇頌和韓公廉利用天衡裝置製造的水運儀象台，就是一個按負反饋原理構成的閉環非線性自動控制系統。上層是一個露天的平台，設有渾儀一座，用龍柱支持，下面有水槽以定水平。

中層是一間沒有窗戶的密室，裡面放置渾象。天球的一半隱沒在地平之下，另一半露在地平的上面，靠機輪帶動旋轉，一晝夜轉動一圈，真實地再現了星辰的起落等天象的變化。下層包括報時裝置和全台的動力機構等。

2.起步階段

隨著科學技術與工業生產的發展，到十七、十八世紀自動控制技術逐漸應用到現代工業中。1681年法國物理學家、發明家巴本(D. Papin)發明了用做安全調節裝置的鍋爐壓力調節器。1765年俄國人普爾佐諾夫(I. Polzunov)發明了蒸汽鍋爐水位調節器等。1788年，英國人瓦特(J. Watt)在他發明的蒸汽機上使用了離心調速器，解決了蒸汽機的速度控制問題，引起了人們對控制技術的重視。飛球加速器（離心調速器）：就是有兩個飛球，一轉起來以後，因為離心力，飛球就往外脹。飛球脹開以後，這個下面的套筒就往上升，這個套筒在移動，就帶動執行機構動作，這是最早的瓦特的離心調速器。

以後人們曾經試圖改善調速器的準確性，卻常常導致系統產生振蕩。自動控制技術的逐步應用，加速了第一次工業革命的步伐。

3.發展階段

實踐中出現的問題，促使科學家們從理論上進行探索研究。1868年，英國物理學家麥克斯韋(J.C. Maxwell)通過對調速系統線性常微分方程的建 立和分析，解釋了瓦特蒸汽機速度控制系統中出現的劇烈振蕩的不穩定問題，提出了簡單的穩定性代數判據，開闢了用數學方法研究控制系統的途徑。

此後，英國數學家勞斯(E.J. Routh)和德國數學家胡爾維茨(A. Hurwitz)把麥克斯韋的思想擴展到高階微分方程描述的更複雜的系統中，分別在1877年和1895年各自提出了直接根據代數方程的係數判別系統穩定性的準則兩個著名的穩定性判據—勞斯判據和胡爾維茨判據。這些方法基本上滿足了20世紀初期控制工程師的需要，奠定了經典控制理論中時域分析法的基礎。

由於第二次世界大戰需要控制系統具有準確跟蹤與補償能力，1932年美國物理學家奈奎斯特(H. Nyquist)提出了頻域內研究系統的頻率響應法，建立了以頻率特性為基礎的穩定性判據，為具有高質量的動態品質和靜態準確度的軍用控制系統提供了所需的分析工具。隨後，伯德(H.W. Bode)和尼科爾斯(N.B. Nichols)在1930年代末和1940年代初進一步將頻率響應法加以發展，形成了經典控制理論的頻域分析法。建立在奈奎斯特的頻率響應法和伊萬斯的根軌跡法基礎上的理論，稱為 經典控制理論(或稱古典控制理論、自動控制理論)，為工程技術人員提供了一個設計反饋控制系統的有效工具。

4.標誌階段

1947年控制論的奠基人美國數學家維納(N. Weiner)把控制論引起的自動化同第二次產業革命聯繫起來，並於1948年出版了《控制論—關於在動物和機器中控制與通訊的科學》。書中論述了控制理論的一般方法，推廣了反饋的概念，為控制理論這門學科奠定了基礎。

1948年美國科學家伊萬斯(W.R. Evans)創立了根軌跡分析方法，為分析系統性能隨 系統參數變化的規律性提供了有力工具，被廣泛應用於反饋控制系統的分析、設計中。我國著名科學家錢學森將控制理論應用於工程實踐，並與1954年出版了《工程式控制制論》。

從20世紀40年代到50年代末，經典控制理論的發展與應用使整個世界的科學水平出現了巨大的飛躍，幾乎在工業、農業、交通運輸及國防建設的各個領域都廣泛採用了自動化控制技術。

第二次世界大戰期間，反饋控制方法被廣泛用於設計研製飛機自動駕駛儀、火炮定位系統、雷達天線控制系統以及其他軍用系統。這些系統的複雜性和對快速跟蹤、精確控制的高性能追求，迫切要求拓展已有的控制技術，促使了許多新的見解和方法的產生。同時，還促進了對非線性系統、採樣系統以及隨機控制系統的研究。可以說工業革命和戰爭促使了經典控制理論的發展。

以傳遞函數作為描述系統的數學模型，以時域分析法、根軌跡法和頻域分析法為主要分析設計工具，構成了經典控制理論的基本框架。到20世紀50年代，經典控制理論發展到相當成熟的地步，形成了相對完整的理論體系，為指導當時的控制工程實踐發揮了極大的作用。

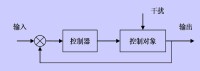
經典控制理論主要用於解決反饋控制系統中控制器的分析與設計的問題。下圖反饋控制系統的簡化原理框圖。以爐溫控制為例，受控對象為爐子；輸出變數為實際的爐子溫度；輸入變數為給定常值溫度，一般用電壓表示。爐溫用熱電偶測量，代表爐溫的熱電動勢與給定電壓相比較，兩者的差值電壓經過功率放大後用來驅動相應的執行機構進行控制。

60年代產生的現代控制理論是以狀態變數概念為基礎，利用現代數學方法和計算機來分析、綜合複雜控制系統的新理論，適用於多輸入、多輸出，時變的或非線性系統。飛行器及其控制系統正是這樣的系統。應用現代控制理論對它進行分析、綜合能使飛行器控制系統的性能達到新的水平。從60年代“阿波羅”號飛船登月，70年代“阿波羅”號飛船與“聯盟”號飛船的對接，直到80年代太空梭的成功飛行，都是與現代控制理論和計算機的應用分不開的。在控制精度方面，應用現代控制理論、計算機和新型元、部件，使洲際導彈的命中精度由幾十公里減小到百米左右。

現代控制理論的核心之一是最優控制理論。這種理論在60年代初開始獲得實際應用。這就改變了經典控制理論以穩定性和動態品質為中心的設計方法，而是以系統在整個工作期間的性能作為一個整體來考慮，尋求最優控制規律，從而可以大大改善系統的性能。最優控制理論用於發動機燃料和轉速控制、軌跡修正最小時間控制、最優航跡控制和自動著陸控制等方面都取得了明顯的成果。

現代控制理論的另一核心是最優估計理論（卡爾曼濾波）。它為解決飛行器控制中的隨機干擾和隨機控制問題提供一種有力的數學工具。卡爾曼濾波突破了維納濾波的局限性，適用於多輸入、多輸出線性系統，平穩或非平穩的隨機過程，在飛行器測軌-跟蹤、控制攔截和會合等方面得到廣泛應用。

現代控制理論所包含的學科內容十分廣泛，主要的方面有：線性系統理論、非線性系統理論、最優控制理論、隨機控制理論和適用控制理論。

線性系統理論 它是現代控制理論中最為基本和比較成熟的一個分支，著重於研究線性系統中狀態的控制和觀測問題，其基本的分析和綜合方法是狀態空間法。按所採用的數學工具，線性系統理論通常分成為三個學派：基於幾何概念和方法的幾何理論，代表人物是W.M.旺納姆；基於抽象代數方法的代數理論，代表人物是R.E.卡爾曼；基於復變數方法的頻域理論，代表人物是H.H.羅森布羅克。

非線性系統理論 非線性系統的分析和綜合理論尚不完善。研究領域主要還限於系統的運動穩定性、雙線性系統的控制和觀測問題、非線性反饋問題等。更一般的非線性系統理論還有待建立。從70年代中期以來，由微分幾何理論得出的某些方法對分析某些類型的非線性系統提供了有力的理論工具。

最優控制理論 最優控制理論是設計最優控制系統的理論基礎，主要研究受控系統在指定性能指標實現最優時的控制規律及其綜合方法。在最優控制理論中，用於綜合最優控制系統的主要方法有極大值原理和動態規劃。最優控制理論的研究範圍正在不斷擴大，諸如大系統的最優控制、分佈參數系統的最優控制等。

隨機控制理論 隨機控制理論的目標是解決隨機控制系統的分析和綜合問題。維納濾波理論和卡爾曼-布希濾波理論是隨機控制理論的基礎之一。隨機控制理論的一個主要組成部分是隨機最優控制，這類隨機控制問題的求解有賴於動態規劃的概念和方法。

適應控制理論 適應控制系統是在模仿生物適應能力的思想基礎上建立的一類可自動調整本身特性的控制系統。適應控制系統的研究常可歸結為如下的三個基本問題：①識別受控對象的動態特性；②在識別對象的基礎上選擇決策；③在決策的基礎上做出反應或動作。

現代控制理論的發展過程

20世紀50年代中期，科學技術及生產力的發展，特別是空間技術的發展，迫切要求解決更複雜的多變數系統、非線性系統的最優控制問題(例如火箭和宇航器的導航、跟蹤和著陸過程中的高精度、低消耗控制，到達目標的控制時間最小等)。實踐的需求推動了控制理論的進步，同時，計算機技術的發展也從計算手段上為控制理論的發展提供了條件，適合於描述航天器的運動規律，又便於計算機求解的狀態空間模型成為主要的模型形式。

俄國數學家李雅普諾夫1892年創立的穩定性理論被引入到控制中。1956年，美國數學家貝爾曼(R. Bellman)提出了離散多階段決策的最優性原理，創立了動態規劃。之後，貝爾曼等人提出了狀態分析法；並於1964年將離散多階段決策的動態規劃法解決了連續動態系統的最優控制問題。美國數學家卡爾曼(R. Kalman)等人於1959年提出了著名的卡爾曼濾波器，1960年又在控制系統的研究中成功地應用了狀態空間法，提出系統的能控性和能觀測性問題。1956年，前蘇聯科學家龐特里亞金(L.S. Pontryagin)提出極大值原理，並於1961年證明並發表了極大值原理。極大值原理和動態規劃為解決最優控制問題提供了理論工具。

到1960年代初，一套以狀態方程作為描述系統的數學模型，以最優控制和卡爾曼濾波為核心的控制系統分析、設計的新原理和方法基本確定，現代控制理論應運而生。進入20世紀60年代，英國控制理論學者羅森布洛克(H.H. Rosenbrock)、歐文斯(D.H. Owens)和麥克法輪(G.J. MacFarlane)研究了使用於計算機輔助控制系統設計的現代頻域法理論，將經典控制理論傳遞函數的概念推廣到多變數系統，並探討了傳遞函數矩陣與狀態方程之間的等價轉換關係，為進一步建立統一的線性系統理論奠定了基礎。

20世紀70年代瑞典控制理論學者奧斯特隆姆(K.J. Astrom)和法國控制理論學者朗道(L.D. Landau)在自適應控制理論和應用方面作出了貢獻。與此同時，關於系統辨識、最優控制、離散時間系統和自適應控制的發展大大豐富了現代控制理論的內容。現代控制理論主要利用計算機作為系統建模分析、設計乃至控制的手段，適用於多變數、非線性、時變系統。它在本質上是一種“時域法”但並不是對經典頻域法的從頻率域回到時間域的簡單再回歸，而是立足於新的分析方法，有著新的目標的新理論。現代控制理論研究內容非常廣泛，主要包括三個基本內容：多變數線性系統理論、最優控制理論以及最優估計與系統辨識理論。從理論上解決了系統的能控性、能觀測性、穩定性以及許多複雜系統的控制問題。

1、不僅適用於SISO線性定常系統，而且易於推廣到MIMO系統、時變系統和非線性系統等，顯示了該方法有更強的描述系統的動態特性行為的能力，所能處理的系統的範圍更大。

2、利用時間域法容易給人以時間上的清晰性能指標，如最快、最小能量等，易於理解接受和優化設計。

3、易於考慮系統的初始條件，使得所設計的控制系統有更高的精度和更佳的性能品質指標。

4、易於用計算機進行系統分析計算和實現計算機控制，顯示了所設計的控制系統的實現具有極大的可行性、優越性、先進性。

複雜系統控制理論與應用：採用結構分散化方法研究複雜系統的建模與控制問題，以結構分散化模型為基礎，研究新的系統辨識理論和新的控制方法。

智能控制理論研究與應用：在對模糊控制、神經網路、專家系統和遺傳演演算法等理論進行分析和研究的基礎上，重點研究多種智能方法綜合應用的集成智能控制演演算法。

計算機控制系統：針對不同的生產過程和控制對象，研究採用DCS、PLC、工業控制計算機等控制設備，構成低成本、高性能、多功能的計算機控制系統。

網路控制理論及其應用：通過對網路拓撲結構及網路環境下先進控制理論與方法的研究，充分利用網路資源，實現從決策到控制的全過程優化。

建立在狀態空間法基礎上的一種控制理論，是自動控制理論的一個主要組成部分。在現代控制理論中，對控制系統的分析和設計主要是通過對系統的狀態變數的描述來進行的，基本的方法是時間域方法。現代控制理論比經典控制理論所能處理的控制問題要廣泛得多，包括線性系統和非線性系統，定常系統和時變系統，單變數系統和多變數系統。它所採用的方法和演演算法也更適合於在數字計算機上進行。現代控制理論還為設計和構造具有指定的性能指標的最優控制系統提供了可能性。現代控制理論的名稱是在1960年以後開始出現的，用以區別當時已經相當成熟並在後來被稱為經典控制理論的那些方法。現代控制理論已在航空航天技術、軍事技術、通信系統、生產過程等方面得到廣泛的應用。現代控制理論的某些概念和方法，還被應用於人口控制、交通管理、生態系統、經濟系統等的研究中。

現代控制理論是在20世紀50年代中期迅速興起的空間技術的推動下發展起來的。空間技術的發展迫切要求建立新的控制原理，以解決諸如把宇宙火箭和人造衛星用最少燃料或最短時間準確地發射到預定軌道一類的控制問題。這類控制問題十分複雜，採用經典控制理論難以解決。1958年，蘇聯科學家Л.С.龐特里亞金提出了名為極大值原理的綜合控制系統的新方法。在這之前，美國學者R.貝爾曼於1954年創立了動態規劃，並在1956年應用於控制過程。他們的研究成果解決了空間技術中出現的複雜控制問題，並開拓了控制理論中最優控制理論這一新的領域。1960～1961年，美國學者R.E.卡爾曼和R.S.布希建立了卡爾曼-布希濾波理論，因而有可能有效地考慮控制問題中所存在的隨機雜訊的影響，把控制理論的研究範圍擴大，包括了更為複雜的控制問題。幾乎在同一時期內，貝爾曼、卡爾曼等人把狀態空間法系統地引入控制理論中。狀態空間法對揭示和認識控制系統的許多重要特性具有關鍵的作用。其中能控性和能觀測性尤為重要，成為控制理論兩個最基本的概念。到60年代初，一套以狀態空間法、極大值原理、動態規劃、卡爾曼-布希濾波為基礎的分析和設計控制系統的新的原理和方法已經確立，這標誌著現代控制理論的形成。