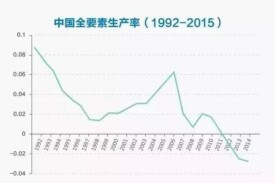
全要素生產率
生產單位作為系統中的各個要素的綜合生產率
全要素生產率 指生產單位(主要為企業)作為系統中的各個要素的綜合生產率,以區別於要素生產率(如技術生產率)。
全要素生產率指生產單位(主要為企業)作為系統中的各個要素的綜合生產率,以區別於要素生產率(如技術生產率)。事實上企業生產率是企業技術升級、管理模式改進、產品質量提高、企業結構升級的綜合功能,任何現實的生產率實際上都是全要素生產率。全要素生產率也可以稱之為系統生產率。全要素生產率就是生產力。全要素生產率提高就是產業升級與生產力的發展。
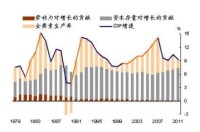
全要素生產率

全要素生產率
50年代,諾貝爾經濟學獎獲得者羅伯特·M·索洛(Robert Merton Solow)提出了具有規模報酬不變特性的總量生產函數和增長方程,形成了通常所說的生產率(全要素生產率)含義,並把它歸結為是由技術進步而產生的。
全要素生產率是宏觀經濟學的重要概念,也是分析經濟增長源泉的重要工具,尤其是政府制定長期可持續增長政策的重要依據。首先,估算全要素生產率有助於進行經濟增長源泉分析,即分析各種因素(投入要素增長、技術進步和能力實現等)對經濟增長的貢獻,識別經濟是投入型增長還是效率型增長,確定經濟增長的可持續性。其次,估算全要素生產率是制定和評價長期可持續增長政策的基礎。具體來說,通過全要素生產率增長對經濟增長貢獻與要素投入貢獻的比較,就可以確定經濟政策是應以增加總需求為主還是應以調整經濟結構、促進技術進步為主。

全要素生產率
全部要素的生產率(TFP)無法從總產量中直接計算出來,故只能採取間接的辦法:
GY=GA+aGL+bGK
其中:GY——經濟增長率
GA——全要素生產率增長率(又稱索洛余值 技術進步率)
GL——勞動增加率
GK——資本增長率
a——勞動份額
b——資本份額

全要素生產率
(一)增長會計法
增長會計法(growth accounting approach) 的基本思路是以新古典增長理論為基礎,將經濟增長中要素投入貢獻剔除掉,從而得到全要素生產率增長的估算值,其本質是一種指數方法。按照指數的不同構造方式,可分為代數指數法和幾何指數法(也稱索洛殘差法)。
1. 代數指數法(AIN)
代數指數法(arithmetic index number approach,AIN) 最早由艾布拉姆威茲(Abramvitz,1956)提出,其基本思想是把全要素生產率表示為產出數量指數與所有投入要素加權指數的比率。
假設商品價格為Pt,數量為Qt,則總產出為PtQt。生產中資本投入為Kt,勞動投入為Lt,資本價格即利率為rt,工資率為wt,則總成本為rtKt +wtLt。在完全競爭和規模收益不變假設下,有總產出等於總成本即:
PtQt =rtKt +wtLt⑴
但由於技術進步等因素的影響,⑴ 式往往不成立,可將⑴ 式改寫為:
PQt =TFPt[rKt +wLt]⑵
其中,r0 、w0 和P0 為基年利率、工資和價格。參數TFPt 為全要素生產率,反映技術進步等因素對產出的影響。
TFPt=PQt/[rKt +wLt] (3)
⑶ 式就是全要素生產率的代數指數公式。後來,經濟學家們又提出各種全要素生產率代數指數,它們的形式雖不同,但基本思想是一樣的。
代數指數法很直觀地體現出全要素生產率的內涵,但缺陷也十分明顯,主要體現在它雖然沒有明確設定生產函數,但暗含著資本和勞動力之間完全可替代,且邊際生產率是恆定的,這顯然缺乏合理性。所以這種方法更多地是一種概念化方法,並不適於具體實證分析(Caves,Christensen andDiewart,1982)。
2.索洛殘差法(SR)
索洛殘差法最早由羅伯特·索洛(Robert Merton Solow,1957)提出,基本思路是估算出總量生產函數后,採用產出增長率扣除各投入要素增長率后的殘差來測算全要素生產率增長,故也稱生產函數法。在規模收益不變和希克斯中性技術假設下,全要素生產率增長就等於技術進步率。總量生產函數為:
Yt = Ω(t)F(Xt) ⑷
其中,Yt為產出,xnt為第n 種投入要素。假設Ω(t) 為希克斯中性技術係數,意味著技術進步不影響投入要素之間的邊際替代率。
TFPt=Ω(t)=Yt/F(Xt)=Yt/(K^α)(L^β) (5)
其中TFPt為全要素生產率,F(Xt)=(K^α)(L^β)為要素投入函數。因此有全要素的增長率tfp為
tfp=(TFPt/TFPt-1)-1 (6)
lnY=lnΩ(t)+αlnKt+βlnLt (8)
這是一個雙對數模型,可以利用OLS 估算。其中資本存量需要測算,測算公式為:
Kt =It /Pt+ (1-δt)Kt-1 (7)
其中Kt 為t 年的實際資本存量,Kt -1 為t - 1 年的實際資本存量,Pt 為固定資產投資價格指數,It 為t 年的名義投資,δt 為t 年的固定資產的折舊率。在確定了資本存量的初值以及實際凈投資后,便可以利用⑺ 式給出各年的實際資本存量。這樣,利用回歸方程⑻,人們可以估計出平均資本產出份額α和平均勞動力產出份額β,帶入(5)和⑹ 式可以得到全要素生產率增長率。索洛殘差法開創了經濟增長源泉分析的先河,是新古典增長理論的一個重要貢獻(Lucas,1988)。但它也存在著一些明顯缺陷:索洛殘差法建立在新古典假設即完全競爭、規模收益不變和希克斯中性技術基礎上,這些約束條件很強,往往難以滿足;具體估算中,由於資本價格難以準確確定,所以利用資本存量來代替資本服務,忽略了新舊資本設備生產效率的差異以及能力實現的影響。此外,索洛殘差法用所謂的“殘差”來度量全要素生產率,從而無法剔除掉測算誤差的影響。上述這些因素都不可避免地導致全要素生產率的估算偏差。
(二)經濟計量法
由於增長會計法存在著較多缺陷,後人提出很多經濟計量方法,以期藉助各種經濟計量模型和計量工具準確地估算出全要素生產率。本文主要比較兩種計量方法,即隱性變數法和潛在產出法。
1.隱性變數法(LV)
隱性變數法(latent variable approach,LV) 的基本思路是,將全要素生產率視為一個隱性變數即未觀測變數,從而藉助狀態空間模型(state space model) 利用極大似然估計給出全要素生產率估算。具體估算中,為了避免出現偽回歸,需要進行模型設定檢驗包括數據平穩性檢驗和協整檢驗。平穩性檢驗和協整檢驗的方法很多,常見的有ADF (the Augmented Dickey2Fuller) 單位根檢驗和JJ(Johanson and Juselius,1990)協整檢驗。由於產出、勞動力和資本存量數據的趨勢成分通常是單位根過程且三者之間不存在協整關係,所以往往利用產出、勞動力和資本存量的一階差分序列來建立回歸方程。
2.潛在產出法(PO)
索洛殘差法和隱性變數法在估算全要素生產率時,都暗含著一個重要的假設即認為經濟資源得到充分利用,此時,全要素生產率增長就等於技術進步率。換言之,這兩種方法在估算全要素生產率時,都忽略了全要素生產率增長的另一個重要組成部分———能力實現改善(improvement incapacity realization) 即技術效率提升的影響。潛在產出法(potential output approach,PO) 也稱邊界生產函數法(frontier production function) 正是基於上述考慮提出的,其基本思路是遵循法雷爾(Farrell,1957)的思想,將經濟增長歸為要素投入增長、技術進步和能力實現改善(技術效率提升)三部分,全要素生產率增長就等於技術進步率與能力實現率改善之和;估算出能力實現率和技術進步率,便給出全要素生產率增長率
如果在生產中投入勞動、資本(包括廠房、機器設備、存貨等勞動創造的資本財物)、土地(包括一切自然資源在內)等生產要素共計100萬美元,而生產出來的總產量為150萬美元。那麼,這150萬美元的產量是由兩個方面的貢獻構成的,其中100萬美元是由於投入了100萬美元的生產要素所引起的,其餘50萬美元則是全要素生產率(TFP)的貢獻。如果本年度的產量比上年度增長15%,而其中要素投入量的增長為10%,則其餘5%就是全要素生產率的增長。