共找到2條詞條名為均勻分佈的結果 展開
- 數學概率論中的術語
- 均勻分配
均勻分佈
數學概率論中的術語
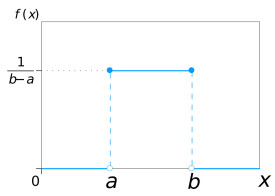
在概率論和統計學中,均勻分佈也叫矩形分佈,它是對稱概率分佈,在相同長度間隔的分佈概率是等可能的。均勻分佈由兩個參數a和b定義,它們是數軸上的最小值和最大值,通常縮寫為U(a,b)。
均勻分佈的概率密度函數為:
在兩個邊界a和b處的f(x)的值通常是不重要的,因為它們不改變任何 的積分值。概率密度函數有時為0,有時為。在傅里葉分析的概念中,可以將f(a)或f(b)的值取為,因為這種均勻函數的許多積分變換的逆變換都是函數本身。
對於平均值μ和方差,概率密度可以寫為:
累積分佈函數為:
它的逆是:
力矩生成函數:
我們可以從中計算原始力矩:
對於特殊情況那麼,
力矩生成函數的簡單形式:對於該分佈的隨機變數,期望值為,方差為。
一階矩(均值):
二階中心矩(方差):
也可以用期望來求:
令 是服從於的樣本。令X(k)為該樣本的第k次統計量。那麼X(k)的概率分佈是參數為k和的β分佈。期望值是:
方差是:
均勻分佈的隨機變數落在固定長度的任何間隔內的概率與區間本身的位置無關(但取決於間隔大小),只要間隔包含在分佈的支持中即可。
為了看到這一點,如果並且是具有固定的[a,b]的子間隔,則
若並且,所得分佈稱為標準均勻分佈。
標準均勻分佈的一個有趣的屬性是,如果具有標準均勻分佈,那麼也是如此。
(1)如果X服從標準均勻分佈,則通過逆變換方法,具有指數分佈參數。
(2)如果X服從標準均勻分佈,則具有參數(,1)的β分佈。
(3)如果X服從標準均勻分佈,則也是具有參數(1,1)的β分佈的特殊情況。
(4)兩個獨立的,均勻分佈的總和產生對稱的三角分佈。
統計學中,當使用p值作為簡單零假設的檢驗統計量,並且檢驗統計量的分佈是連續的,則如果零假設為真,則p值均勻分佈在0和1之間。
如果u是從標準均勻分佈中採樣的值,則如上所述,的值遵循由a和b參數化的均勻分佈。
均勻分佈對於任意分佈的採樣是有用的。一般的方法是使用目標隨機變數的累積分佈函數(CDF)的逆變換採樣方法。這種方法在理論工作中非常有用。由於使用這種方法的模擬需要反轉目標變數的CDF,所以已經設計了cdf未以封閉形式知道的情況的替代方法。一種這樣的方法是拒收抽樣。
正態分佈是逆變換方法效率不高的重要例子。然而,有一個確切的方法,Box-Muller變換,它使用逆變換將兩個獨立的均勻隨機變數轉換成兩個獨立的正態分佈隨機變數。
在模數轉換中,發生量化誤差。該錯誤是由於四捨五入或截斷。當原始信號比一個最低有效位(LSB)大得多時,量化誤差與信號不顯著相關,並具有大致均勻的分佈。因此,RMS誤差遵循該分佈的方差。