譜半徑
譜半徑
在數學中,矩陣或者有界線性運算元的譜半徑是指其特徵值集合的上確界,一般寫作ρ(·)。
令λ1, ..., λn是矩陣A ∈ Cⁿ×ⁿ中的特徵值,則其譜半徑 ρ(A) is 定義為: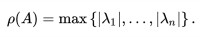
譜半徑
A的條件數可以用譜半徑表示,公式為ρ(A)ρ(A⁻¹)。
譜半徑是矩陣所有范數的一種下確界(infimum)。另一方面, ρ(A)≤||A||對每一個矩陣范數||·||都成立,Gelfand公式指出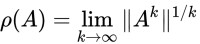
譜半徑
。不過,針對任意向量v∈Cⁿ,譜半徑不一定會滿足||Av||≤ρ(A)||v||。若要說明原因,可以令r>1為任意數,考慮矩陣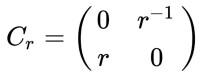 。Cᵣ 的特徵多項式是λ²-1,因此其特徵值為±1,且ρ(Cᵣ)=1。不過Cᵣe₁=re₂,因此||Cᵣe₁||=r>1=ρ(Cᵣ)||e₁||,其中||·||是Cⁿ上的任何ιᴾ范數。至於可以當k→∞時,讓
。Cᵣ 的特徵多項式是λ²-1,因此其特徵值為±1,且ρ(Cᵣ)=1。不過Cᵣe₁=re₂,因此||Cᵣe₁||=r>1=ρ(Cᵣ)||e₁||,其中||·||是Cⁿ上的任何ιᴾ范數。至於可以當k→∞時,讓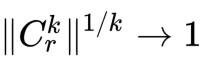 的原因是C²ᵣ=I,因此當k→∞時,使
的原因是C²ᵣ=I,因此當k→∞時,使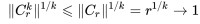 ||Av||≤ρ(A)||v||針對所有v∈Cⁿ成立的條件是A為埃爾米特矩陣及||·||為歐幾里得范數。
||Av||≤ρ(A)||v||針對所有v∈Cⁿ成立的條件是A為埃爾米特矩陣及||·||為歐幾里得范數。
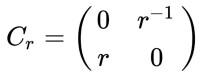
譜半徑
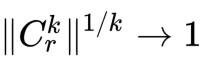
譜半徑
譜半徑
有限圖的譜半徑定義為其鄰接矩陣的譜半徑。
此一定義可以擴散到無限圖,但是其每個頂點都只連接有限個頂點(存在一實數C使得每一個頂點的度都小於C)。此情形下,針對圖G可定義:
譜半徑
譜半徑
以下的命題指出了一個簡單但是有用的矩陣譜半徑上界:
命題:令A ∈ Cⁿ×ⁿ,其譜半徑為ρ(A),以及相容(Consistent)矩陣范數 ||⋅||。則針對每一個整數k≥1:
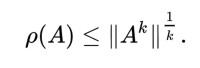
譜半徑
令(v, λ)為矩陣A的特徵值-特徵向量對。利用矩陣范數的次可乘性(sub-multiplicative property),可得:
譜半徑
因為v ≠ 0,可得
|λ|ᵏ≤||Aᵏ||
因此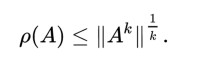
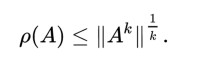
譜半徑
有關n個頂點,m個邊的圖,有許多的譜半徑的上界公式。例如,若
譜半徑
譜半徑
譜半徑和矩陣乘冪數列是否收斂有緊密的關係。以下的定理會成立:
定理:令A ∈ Cⁿ×ⁿ,其譜半徑ρ(A)。則ρ(A) < 1當且僅當
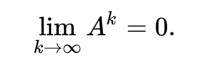
譜半徑
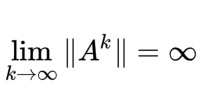
譜半徑
假設問題中的極限值為零,可以證明ρ(A) < 1。令(v, λ)為A的特徵值和特徵向量對。因為Aᵏv = λᵏv可得:
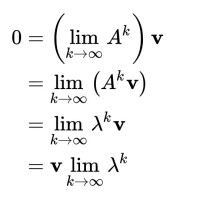
譜半徑
因為假設v ≠ 0,會得到
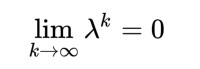
譜半徑
接下來假設A的譜半徑小於1。根據若爾當標準型定理,可以知道針對所有的A ∈ C,存在V, J ∈ C以及非奇異的V和J分塊對角矩陣使得:
A=VJV⁻¹而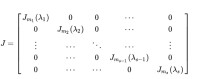
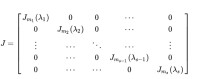
譜半徑
其中,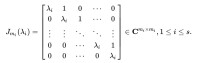 因此可得
因此可得
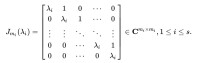
譜半徑
Aᵏ=VJᵏV⁻¹
因為J是分塊對角矩陣
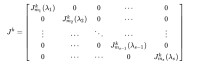
譜半徑
而mᵢ×mᵢ若爾當方塊矩陣k次方可以得到,針對k≥mᵢ-1:
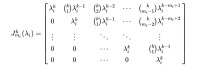
譜半徑
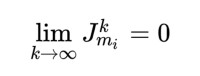
譜半徑
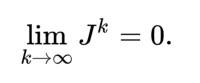
譜半徑
因此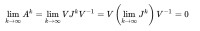
譜半徑
另一方面,若ρ(A)>1,當k增加時,在J中至少有一個元素無法維持有界,因此證明了定理的第二部分。