方塊矩陣
方塊矩陣
方塊矩陣,或簡稱方陣,是行數及列數皆相同的矩陣。由n*n矩陣組成的集合,連同矩陣加法和矩陣乘法,構成環。除了 n = 1,此環並不是交換環。
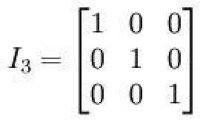
方塊矩陣
單位矩陣 In 的對角線全是 1 而其他位置全是 0,對所有M*N矩陣 M 及N*K矩陣 N 都有 MIn = M 及 InN = N。
例如,若 n = 3:
單位矩陣是方塊矩陣環的單位元。
方塊矩陣環的可逆元稱為可逆矩陣或非奇異矩陣。 N*N矩陣 A 是可逆當且僅當存在矩陣 B 使得
AB = In( = BA)。
此時 B 稱為 A 的逆矩陣,並記作 A − 1。所有N*N矩陣在乘法上組成一個群(亦是一個李群),稱為一般線性群。
若數字 λ 和非零向量V滿足,則AV=λV(V為向量)為 A 的一個特徵向量,λ 是其對應的特徵值。數字 λ 為 A 的特徵值當且僅當 A − λIn 可逆,又當且僅當 pA(λ) = 0。這裡,pA(x) 是 A 的特徵多項式。特徵多項式是一個 n 次多項式,有 n 個復根(考慮重根),即 A 有 n 個特徵值。
方塊矩陣 A 的行列式是其 n 個特徵值的積, 但亦可經由Leibniz formula計算出來。可逆矩陣正好是那些行列式非零的矩陣.
高斯-若爾當消元法非常重要,可以用來計算矩陣的行例式,秩,逆矩陣,並解決線性方程組。
矩陣的跡是N*N矩陣的對角線元素之和,也是其 n 個特徵值之和。
所有正交矩陣都是方塊矩陣。