康托爾-伯恩施坦定理
康托爾-伯恩施坦定理
康托爾-伯恩施坦定理也叫作定理康托爾-伯恩斯坦-施羅德定理(Cantor-Bernstein-Schroeder theorem),是集合論中的一個基本定理,得名於康托爾、伯恩斯坦和 Ernst Schröder。
康托爾-伯恩斯坦定理(Cantor-Bernstein theorem)是集合論中的一個基本定理,得名於康托爾、伯恩斯坦和 Ernst Schröder。該定理陳述說:如果在集合A和B之間存在單射和,則存在一個雙射。從勢的角度來看, 這意味著如果 並且,則 ,即A與B等勢。顯然,這是在基數排序中非常有用的特徵。
下面是證明:
證明:令
並令
對任意的a∈A定義映射
如果a不在集合C中,那麼a不在集合C中。因此由C的定義可知。由於g是單射,其逆映射g(a)存在。
接下來驗證就是想要的雙射。
• 滿射:對任何,如果,那麼存在使得。因此由h的定義可知。如果,定義。由C的定義知,a不屬於C。由於f[C] 是f[C]的一個子集,因而b不屬於任何一個f[C],所以由集合C的遞歸定義知, 不屬於此處錯誤,邏輯反了*。因此,a不屬於C。那麼根據h的定義。
• 單射:若,則有四種情況。對於前兩種情況,由f與g是單射得。對於第三種情況,有,又由前提,而C在g°f下封閉,於是,但是由前提得,矛盾了,因此第三種情況不可能出現。同理第四種情況也不可能出現,這說明。綜上若,一定有。
注意這個h的定義是非構造性的,在這個意義下:不存在一般性方法在有限步驟內判定,對於任何給定集合A和B與單射f和g,是否A的一個元素x不位於C中。對於特殊集合和映射這當然是可能的。
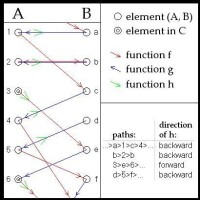
圖1.h的定義
顯示的是部分的(不相交)集合A和B,以及映射f和g的一部分。如果集合A∪B,與兩個映射一起,被詮釋為一個有向圖,則這個雙向圖有多個連接起來的構件(component)。
這些可以分成四個類型:無限擴展到兩個方向的路徑,偶數長度的有限圈(環),開始於集合A中的無限路徑,和開始於集合B中的無限路徑(在圖中通過元素a的路徑是在兩個方向上無限的,所以這個圖包含每個類型的一個路徑)。一般的說,不可能在有限步驟內判定A或B的一個給定元素屬於那種類型的路徑。
上面定義的集合C恰好包含了那些開始在A中的無限路徑所經過的A的元素。映射h接著被按如下方式定義,對於所有路徑它生成一個雙射,把在路徑中A的每個元素,映射到在路徑中直接前於或後於它的B的一個元素。對於在兩個方向上都是無限的路徑,和對於有限圈,我們選擇映射所有元素到它在路徑中的前驅。
這個定理也叫做 Schroeder-Bernstein 定理,但一般會加上康托爾的名字,畢竟他貢獻了最初的版本。它也叫做 Cantor-Bernstein 定理。