排隊論

日常生活中存在大量有形和無形的排隊或擁擠現象，如旅客購票排隊，市內電話佔線等現象。排隊論的基本思想是1909年丹麥數學家、科學家，工程師A.K.埃爾朗在解決自動電話設計問題時開始形成的，當時稱為話務理論。他在熱力學統計平衡理論的啟發下，成功地建立了電話統計平衡模型，並由此得到一組遞推狀態方程，從而導出著名的埃爾朗電話損失率公式。

自20世紀初以來，電話系統的設計一直在應用這個公式。30年代蘇聯數學家А.Я.欣欽把處於統計平衡的電話呼叫流稱為最簡單流。瑞典數學家巴爾姆又引入有限後效流等概念和定義。他們用數學方法深入地分析了電話呼叫的本徵特性，促進了排隊論的研究。50年代初，美國數學家關於生滅過程的研究、英國數學家D.G.肯德爾提出嵌入馬爾可夫鏈理論，以及對排隊隊型的分類方法，為排隊論奠定了理論基礎。在這以後，L.塔卡奇等人又將組合方法引進排隊論，使它更能適應各種類型的排隊問題。70年代以來，人們開始研究排隊網路和複雜排隊問題的漸近解等，成為研究現代排隊論的新趨勢。

排隊論(queuing theory),或稱隨機服務系統理論，是通過對服務對象到來及服務時間的統計研究，得出這些數量指標（等待時間、排隊長度、忙期長短等）的統計規律，然後根據這些規律來改進服務系統的結構或重新組織被服務對象，使得服務系統既能滿足服務對象的需要，又能使機構的費用最經濟或某些指標最優。它是數學運籌學的分支學科。也是研究服務系統中排隊現象隨機規律的學科。廣泛應用於計算機網路,生產,運輸,庫存等各項資源共享的隨機服務系統。排隊論研究的內容有3個方面：統計推斷，根據資料建立模型；系統的形態，即和排隊有關的數量指標的概率規律性；系統的優化問題。其目的是正確設計和有效運行各個服務系統，使之發揮最佳效益。

排隊論起源於20世紀初的電話通話。1909—1920年丹麥數學家、電氣工程師愛爾蘭（A.K.Erlang）用概率論方法研究電話通話問題，從而開創了這門應用數學學科，並為這門學科建立許多基本原則。20世紀30年代中期，當費勒(W.Feller)引進了生滅過程時，排隊論才被數學界承認為一門重要的學科。在第二次世界大戰期間和第二次世界大戰以後，排隊論在運籌學這個新領域中變成了一個重要的內容。20世紀50年代初，堪道爾(D.G.Kendall)對排隊論作了系統的研究，他用嵌入馬爾柯夫(A.A.Markov)鏈方法研究排隊論，使排隊論得到了進一步的發展。是他首先（1951年）用3個字母組成的符號A/B/C表示排隊系統。其中A表示顧客到達時間分佈，B表示服務時間的分佈，C表示服務機構中的服務台的個數。

1、排隊模型的表示

X/Y/Z/A/B/C

X—顧客相繼到達的間隔時間的分佈；

Y—服務時間的分佈；

M—負指數分佈、D—確定型、Ek—k階愛爾蘭分佈；

Z—服務台個數；

A—系統容量限制（默認為∞）；

B—顧客源數目（默認為∞）；

C—服務規則（默認為先到先服務FCFS)。

2、排隊系統的衡量指標

服務隊長Ls—服務中的顧客數；

排隊長Lq—隊列中的顧客數；

總隊長L=Ls+Lq系統中的顧客總數；

逗留時間Ws—顧客在服務中的等待時間；

等待時間Wq—顧客在隊列中的等待時間；

總時間W=Ws+Wq顧客在系統中的總停留時間；

忙期—服務機構兩次空閑的時間間隔；

服務強度ρ；

穩態—系統運行充分長時間后，初始狀態的影響基本消失，系統狀態不再隨時間變化。

3、到達間隔時間與服務時間的分佈

泊松分佈；

負指數分佈；

愛爾蘭分佈；

統計數據的分佈判斷。

排隊系統的構成及應用前景

排隊系統由輸入過程與到達規則、排隊規則、服務機構的結構、服務時間與服務規劃組成。

一般還假設到達間隔時間序列與服務時間均為獨立同分佈隨機變數序列，且這兩個序列也相互獨立。

評價一個排隊系統的好壞要以顧客與服務機構兩方面的利益為標準。就顧客來說總希望等待時間或逗留時間越短越好，從而希望服務台個數儘可能多些但是，就服務機構來說，增加服務台數，就意味著增加投資，增加多了會造成浪費，增加少了要引起顧客的抱怨甚至失去顧客，增加多少比較好呢？顧客與服務機構為了照顧自己的利益對排隊系統中的3個指標：隊長、等待時間、服務台的忙期（簡稱忙期）都很關心。因此這3個指標也就成了排隊論的主要研究內容。

排隊論的應用非常廣泛。它適用於一切服務系統。尤其在通信系統、交通系統、計算機、存貯系統、生產管理系統等方面應用得最多。排隊論的產生與發展來自實際的需要，實際的需要也必將影響它今後的發展方向。

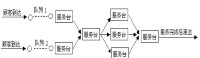
排隊系統又稱服務系統。服務系統由服務機構和服務對象（顧客）構成。服務對象到來的時刻和對他服務的時間（即佔用服務系統的時間）都是隨機的。圖1為一最簡單的排隊系統模型。排隊系統包括三個組成部分：輸入過程、排隊規則和服務機構。

輸入過程考察的是顧客到達服務系統的規律。它可以用一定時間內顧客到達的數量或前後兩個顧客相繼到達的間隔時間來描述，一般分為確定型和隨機型兩種。例如，在生產線上加工的零件按規定的間隔時間依次到達加工地點，定期運行的班車、班機等都屬於確定型輸入。隨機型的輸入是指在時間t內顧客到達數n（t）服從一定的隨機分佈。如服從泊松分佈，則在時間t內到達n個顧客的概率為或相繼到達的顧客的間隔時間T服從負指數分佈，即

式中λ為單位時間顧客期望到達數，稱為平均到達率；1/λ為平均間隔時間。在排隊論中，討論的輸入過程主要是隨機型的。

排隊規則分為等待制、損失制和混合制三種。當顧客到達時，所有服務機構都被佔用，則顧客排隊等候，即為等待制。在等待制中，為顧客進行服務的次序可以是先到先服務，或後到先服務，或是隨機服務和有優先權服務（如醫院接待急救病人）。如果顧客來到后看到服務機構沒有空閑立即離去，則為損失制。有些系統因留給顧客排隊等待的空間有限，因此超過所能容納人數的顧客必須離開系統，這種排隊規則就是混合制。

可以是一個或多個服務台。多個服務台可以是平行排列的，也可以是串連排列的。服務時間一般也分成確定型和隨機型兩種。例如，自動沖洗汽車的裝置對每輛汽車沖洗（服務）時間是相同的，因而是確定型的。而隨機型服務時間v則服從一定的隨機分佈。如果服從負指數分佈，則其分佈函數是

式中μ為平均服務率，1/μ為平均服務時間。

如果按照排隊系統三個組成部分的特徵的各種可能情形來分類，則排隊系統可分成無窮多種類型。因此只能按主要特徵進行分類。一般是以相繼顧客到達系統的間隔時間分佈、服務時間的分佈和服務台數目為分類標誌。現代常用的分類方法是英國數學家D.G.肯德爾提出的分類方法，即用肯德爾記號X/Y/Z進行分類。

X處填寫相繼到達間隔時間的分佈；

Y處填寫服務時間分佈;

Z處填寫並列的服務台數目。

各種分佈符號有：M-負指數分佈;D-確定性;Ek-k階埃爾朗分佈；GI-一般相互獨立分佈；G-一般隨機分佈等。這裡k階埃爾朗分佈是為相互獨立且服從相同指數分佈的隨機變數時服從自由度為2k的χ2分佈。例如,M/M/1表示顧客相繼到達的間隔時間為負指數分佈、服務時間為負指數分佈和單個服務台的模型。D/M/C表示顧客按確定的間隔時間到達、服務時間為負指數分佈和C個服務台的模型。至於其他一些特徵，如顧客為無限源或有限源等，可在基本分類的基礎上另加說明。

研究排隊系統問題的主要目的是研究其運行效率，考核服務質量，以便據此提出改進措施。通常評價排隊系統優劣的有6項數量指標。

①系統負荷水平ρ：它是衡量服務台在承擔服務和滿足需要方面能力的尺度；

②系統空閑概率P0：系統處於沒有顧客來到要求服務的概率；

③隊長：系統中排隊等待服務和正在服務的顧客總數，其平均值記為LS；

④隊列長：系統中排隊等待服務的顧客數，其平均值記為Lg；

⑤逗留時間：一個顧客在系統中停留時間，包括等待時間和服務時間，其平均值記為WS；

⑥等待時間：一個顧客在系統中排隊等待時間，其平均值記為Wg。M/M/1排隊系統是一種最簡單的排隊系統。系統的各項指標可由圖2中狀態轉移速度圖推算出來（表1）。其他類型的排隊系統的各種指標計算公式則複雜得多，可專門列出計算公式圖表備查。現已開始應用計算機模擬來求解排隊系統問題。

排隊論已廣泛應用於交通系統、港口泊位設計、機器維修、庫存控制和其他服務系統。表2中列出排隊論的應用。