負二項分佈

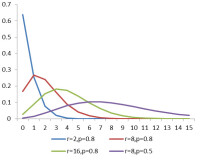
滿足以下條件的稱為負二項分佈

1.實驗包含一系列獨立的實驗。

2.每個實驗都有成功、失敗兩種結果。

3.成功的概率是恆定的。

4.實驗持續到r次成功，r可以為任意正數。

當r是整數時，負二項分佈又稱帕斯卡分佈（巴斯卡分佈），其概率密度函數為（其中一種形式，兩種形式對比看下文）：

它表示，已知一個事件在伯努利試驗中每次的出現概率是p，在一連串伯努利試驗中，一件事件剛好在第r+k次試驗出現第r次的概率。

假設有一組獨立的伯努利數列，每次實驗有兩種結果“成功”和“失敗”。每次實驗的成功概率是p，失敗的概率是1－p。我們得到一組數列，直到預定的失敗數發生r次。那麼結果為“成功”的隨機數X會服從負二項分佈（或帕斯卡）分佈：

X~NB(r;P)

我們在現實生活中也常有應用，成功和失敗的結果可能或者可能不是我們平時所認認為的“好”與“壞”。假設我們把負二項分佈用在一台設備在故障前正常運行的天數的模型，這種情況下，設備一天運行正常，記為結果“成功”，反之故障的話結果為“失敗”。如果我們把負二項分析用在動作員嘗試射門得分前的嘗試次數模型，這種情況下，每次不成功的嘗試在模型里為“成功”，並且得分記為“失敗”。如果我們拋硬幣，負二項分佈可以把頭像一面作為“成功”來記數，在我們提到失敗的結果之前。在下面的概率密度函數里，P是成功的概率，1－p是失敗的概率。

負二項分佈的概率密度函數為：

這裡的括弧里的數為二項分佈的係數，並且等於

該數可以按下面的格式表示，也正是解釋了“負二項”的名字的由來：

為了理解上面的概率密度函數，因為k+r次重複試驗的結果假設是獨立的，需要注意每個特定的k作為成功和r失敗的數列為(1-p)p。因為第r個失敗是最後發生的，所以需要k+r-1次重複實驗中有k次成功的。上面的二項分佈係數，正好它的組合長度為k+r-1。

遞推公式為

舉例說，若我們擲骰子，擲到一即視為成功。則每次擲骰的成功率是1/6。要擲出三次一，所需的擲骰次數屬於集合{3,4,5,6,...}。擲到三次一的擲骰次數是負二項分佈的隨機變數。要在第三次擲骰時，擲到第三次一，則之前兩次都要擲到一，其概率為(1/6)。注意擲骰是伯努利試驗，之前的結果不影響隨後的結果，即每次實驗為獨立隨機實驗。若要在第四次擲骰時，擲到第三次一，則之前三次之中要有剛好兩次擲到一，在三次擲骰中擲到2次1的概率為：

第四次擲骰要擲到一，所以要將前面的概率再乘(1/6)。

參數為(r,p)的負二項分佈的數列k+r的期望是r/(1-p)。為了更直觀的觀察，想象上面的實驗進行了許多次，也就是說，進行特定的實驗直到r個失敗出現，然後另外的一個特定的實驗，然後是另外的實驗，等等。寫下每次實驗的這些嘗試的次數：a,b,c…並且把a+b+c+…=N。現在我們對失敗的預期為N(1-p)。我們說實驗重複了n次，並且總共有有nr個失敗。所以我們估計nr=N(1-p)，所以N/n=r/(1-p)。注意N/n僅僅是平均每個實驗的嘗試次數。這就是我們所說的“期望”。每次實驗的平均成功的嘗試次數為N/n-r，期望值等於r/(1-p)-r=rp/(1-p)。

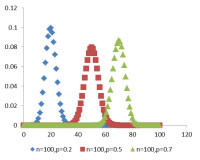
把負二項分佈的定義延伸到到的參數r。儘管很難想象一個非整數的失敗次數，我們仍然可以通過概率密度函數在形式上定義這個分佈。

就像之前，我們說X服從負二項分佈（或者波利亞分佈），如果它有一個如下所示的概率密度函數：

這裡r是一個正實數。通過乘法公式，二項分佈係數可以重新定義，並且可以重新寫成gamma分佈的公式。

注意二項分佈序列和上面的內容里，0≤p≤1.

因此，概率密度函數的項實際上可以合併成一項。

有一些書里的負二項分佈的公式定義可能和這裡的有一些小區別。最常見的變化就是：

X是實驗總次數，得到r個失敗的嘗試。不僅僅是成功的次數。因此，實驗總次數等於失敗數加成功數，這個不同於這裡定義的X。

為了把公式換這種定義進行轉換，把k用k-r代替，並且從均值、中位數，或者眾數中減去r。為了將按本節定義的負二項分佈的公式轉換成本文里的公式，需要用k+r代替k，並且在均值，中位數，眾數中加上r。

這個可能比上面的版本看起來更像二項分佈，注意二項分佈的參數是按順序減少的：最後一個失敗必然在最後發生，所以其它的事件有更少的可利用的位置，在計算順序可能性時。

注意這裡的負二項分佈的定義沒有推廣到正實數r。

P表示失敗的概率，不是成功的。為了把公式進行轉換，每個地方用1-p代替p。X定義為失敗次數，而不是成功的，這裡的定義X為失敗的，但P是成功的，和前面X表示成功但P表示失敗概率的情況用同樣的公式。但是失敗和成功的描述是一致的，並且和前面的進行替換。

這兩個替代公式可能會同時使用，比如X表示總次數，P表示失敗次數。

負二項回歸，分佈是在均值m項里就定義了，並且和線性回歸或者其它的一般線性回歸的解釋變數相關。概率密度函數變為

方差可以寫成m+m/r，參數r參考離散參數，形狀參數，集中係數，或者非均勻或者集中參數。集中參數特別常用於生態學用來描述獨立微生物。減少聚集參數r到0，與增加微生物聚集相一致。0到正無窮的增加相當於沒有聚合，可以被描述成泊松分佈。一些負二項回歸使用r的倒數並且當作分散度參數。

有時候分佈使用均值u和方差σ來參數化分佈，這種情況下：

在r為整數的特定情況下，負二項分佈也可以稱作帕斯卡分佈。它是在獨立重複的伯努利實驗中成功和失敗的數目的概率分佈。因為k+r次概率為p的成功的伯努利實驗可以得到最後一次為失敗的k次成功和r次失敗的概率。換句話說，負二項分佈為成功概率為p的伯努利過程中第r次失敗前的成功次數的概率分佈。一個伯努利過程是離散的過程。因此，實驗次數，失敗、成功次數都是整數。