p級數
調和級數廣義化的結果之一
p級數是調和級數廣義化的其中一個結果,定義如下:公式如圖,其中P是任意正實數。當p=1,p級數即調和級數。由積分判別法或柯西並項判別法(en:Cauchy condensation test(英文))可知p-級數在p>1時收斂(此時級數又叫過調和級數(over-harmonic series)),而在p ≤1時發散。當p>1時,p-級數的和即ζ(p),也就是黎曼ζ函數在p的值。
目錄
數學中的p級數
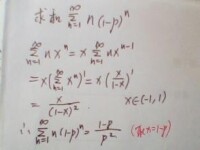
p級數
當時,得到著名的調和級數:。
p級數是重要的正項級數,它是用來判斷其它正項級數斂散性的重要級數。
p級數的斂散性如下:
當時,p級數收斂;
當時,p級數發散。
交錯p級數
形如 的級數稱為交錯p級數。
交錯p級數是重要的交錯級數。
交錯p級數的斂散性如下:
當p>1時,交錯p級數絕對收斂;
當時,交錯p級數條件收斂。
例如,交錯調和級數條件收斂,其和為ln2。
p級數的求和
通過積分轉移、余項逼近的方法,建立起一系列p級數的求和公式,並給出了便於操作的誤差估計方法。一改把級數余項當作誤差來估計的傳統做法,而是將余項作為和的重要組成部分進行分析,使得每增加一項計算量,精度能提升二個以上指數級,從而有效地解決了p級數的求和問題.

