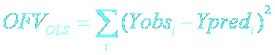群體藥物動力學

群體藥物動力學是研究藥物在某一特定群體中的動力學特徵，通過統計學處理來全面分析藥物與機體的各種相互作用。

1正文 2一. 概念： 3二。群體藥物動力學的研究目的：

4三。群體藥物動力學的特點： 5四. 對藥物體內過程可能產生影響的因素 6五。藥物動力學中的常用研究方法

7六。藥物動力學中模型擬合常用演算法 8七。群體藥物動力學的模型化過程 9八。群體藥物動力學的應用:

正文

群體藥物動力學

一. 概念：

英文為：Population Pharmacokinetics. 國內一般簡寫為：PPK，國外一般為：POP PK，是研究藥物在某一特定群體中的動力學特徵，通過統計學處理來全面分析藥物與機體的各種相互作用。

二。群體藥物動力學的研究目的：

1.觀測病人群體的藥物動力學和藥效動力學的整體特徵。

2.觀察相關因素對於群體藥物動力學和藥效動力學的影響。

3.評估隨機變異性的影響。

三。群體藥物動力學的特點：

1.對於富集數據組與稀疏數據組均可以進行分析

2.應用於臨床前的群體數據分析以及種屬之間的外推

3.可對於不同期或不同次的實驗結果進行同時分析

4.對於相關因素的分析可以為未來的實驗設計，劑量選擇提供指南

5.群體模型的建立可為臨床試驗計劃的模擬提供基礎

6.有助於臨床各期實驗對於藥物動力學－藥效動力學相關關係的研究。

四. 對藥物體內過程可能產生影響的因素

群體藥物動力學的研究對象

(一）.固定效應因素：指可測量，相對穩定的因素

包括：

1. 生理學因素：年齡、性別、體重、種族、肝腎功能、習慣嗜好(煙、酒、茶…)等

2.病理學因素：疾病種類、程度、併發症、合併用藥等

3. 環境因素：實驗人員、場所、時間、藥品批次、來源等

固定效應因素按對藥物體內過程的影響方式，分為：

1. 連續性變化因素－－年齡、體重、肝腎功能等

2. 非連續性變化因素－－種族、嗜好、性別等

(二).隨機效應因素：難以測量，但符合某種分佈特徵

包括：未知的生理病理狀態、無法測定的病理或遺傳學差異、

不易察覺的環境變化、無法避免的測量誤差以及模型偏差。

五。藥物動力學中的常用研究方法

1. 簡單合併數據法 (Naive Pool Data，NPD)

將所有個體的數據合併之後進行處理，彷彿這些數據均來自於同一個體。

2. 簡單平均數據法(Naive Average Data，NAD)

將每個時間點的各個個體的數據平均，然後對此數據進行擬合，求出藥物動力學參數。

3.標準兩步法(Standard Two Stage，STS)

第一步: 對各個體數據分別擬合, 得出每一個體的藥物動力學參數

第二步: 由個體參數求算群體平均, 方差和協方差等。

六。藥物動力學中模型擬合常用演演算法

1.最小二乘法(Ordinary Least Squares, OLS)

群體藥物動力學

2. 擴展最小二乘法 (Extended Least Squares, ELS)

群體藥物動力學

3.貝易斯氏評估法 (Bayesian Estimation)

是群體藥物動力學的有力理論工具

貝易斯定理根據某一事件以往發生的概率特徵 (前置分佈) 來預測其今後發生的可能性 (后發概率)

群體藥物動力學

七。群體藥物動力學的模型化過程

1. 檢視數據

2.基礎結構模型的建立

3.初始結構模型

4.隨機誤差模型

5.群體模型的建立

正向模型化建立全量模型(p<0.05)

逆向模型化建立最終模型(p<0.005)

6.最終模型的校驗

內部驗證

外部驗證

常用的軟體為：NONMEM（nonlinear mixed-effect model)

八。群體藥物動力學的應用:

(一).臨床藥學

治療藥物監測

(二).新葯研究

臨床前以及臨床各期新葯評價

藥物動力學/藥效學模型化

實驗計劃模擬

群體藥物動力學