月形
月形
月形(Tune)有兩種指代,它可以指一種特殊的平面圖形,即同一平面上兩條圓弧之間的(平面)部分,也可以指一種球面圖形,即“球面二角形”。
平面中的月形是一種特殊的平面圖形,指有相同的底,且在底的同一側的兩個弓形弧所圍成的圖形,如圖1中的陰影部分,月形中的一種特殊情形是鐮刀形,即由半圓和扇形的弧所圍成的圖形,如圖2中的陰影部分。
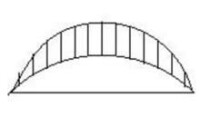
圖1
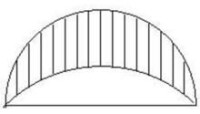
圖2
(新)月形是一種邊緣為兩個圓弧的平面圖形——即月牙形。希波克拉底並沒有作出所有月形的等面積正方形,而只求出了一種他所精心構造的特定月形的面積。希波克拉底的論證是建立在三個初步公理之上的:勾股定理;半圓上的圓周角是直角;兩個圓形或半圓形面積之比等於其直徑的平方比。
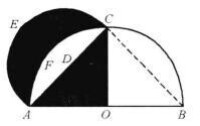
圖3
希波克拉底的證明方法既簡單又高明。首先,他必須證實所論證的新月形與圖中陰影部分的△AOC面積完全相等。這樣,他就可以應用已知的三角形能表示為等價平方的公理來斷定新月形也可用等價平方表示。這一經典論證的詳細過程如下:
由於∠ACB內接於半圓,所以,∠ACB是直角。根據“邊角邊”全等定理,△AOC和△BOC全等,因此AC的長度等於BC的長度,然後根據勾股定理,就得到AB的平方等於AC平方的2倍。因為AB是半圓ACB的直徑,AC是半圓AEC的直徑,所以,我們可以應用上述第三條原理,即得到:
半圓AEC的面積:半圓ACB的面積=AC的平方:AB的平方=1:2。
也就是說,半圓AEC的面積是半圓ACB面積的一半。
我們現在來看扇形AFCO (“扇形”是圓的1/4)。顯然,這一扇形也是半圓ACB面積的一半,據此,我們可直接得出:
半圓AECD的面積=扇形AFCO的面積。
最後,我們只需從這兩個圖形中各自減去它們共同的部分AFCD,如圖4所示,即半圓AEC的面積減去AFCD部分的面積=扇形AFCO的面積減去AFCD部分的面積。
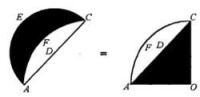
圖4
我們可以作一個正方形,使其面積等於三角形ACO,因而也等於新月形AECF的面積。這就是我們所尋求的化新月形為正方形的問題。
這的確是數學上的一大成就。評註家普羅克洛斯以他5世紀的眼光,認為希俄斯的希波克拉底是一位作圖的天才。
希波克拉底於公元前5世紀生於希俄斯島。關於希波克拉底,我們對他的生平所知甚少。亞里士多德曾寫過,希波克拉底雖然是一位天才的幾何學家,但他看起來在其他方面卻顯得遲鈍又缺乏見識。身為數學家,卻難以應付日常生活,他就是這樣一類人。傳說,希波克拉底是在被強盜騙去錢財后出名的,顯然,他被人當做了容易受騙的傻瓜。為了挽回損失,他前往雅典,並在那裡教學,他是少數幾位為掙錢而開始教學生涯的人物之一”。
希波克拉底對幾何學作出了兩個非凡的貢獻。其一是他編寫了第一部《原本》,第一次闡述了從幾個已知公理或公設中精確而有邏輯性地推導出幾何定理的過程。但遺憾的是,這部書沒有能夠流傳至今。
然而,這部書不論多麼有價值,與100年後歐幾里得的煌煌巨作《幾何原本》相比,也不免黯然失色。歐幾里得的《幾何原本》從根本上宣判了希波克拉底著作的過時。即使如此,我們仍有理由認為,歐幾里得借鑒了他前輩的思想。
令人欣慰的是,希波克拉底的另一個偉大貢獻一新月形面積的求法,卻流傳至今。
公元前5世紀,求平面圖形的面積是古希臘數學家面臨的最嚴重的挑戰。確切地說,一個平面圖形的面積就是只用圓規和直尺作出面積等於原平面圖形的正方形。如果個平面圖形的面積能夠求出,那麼,就認為這個圖形是可用等價平方表示的(或可為平方的)。
求面積問題能夠引起希臘人的興趣並不奇怪。從實踐的觀點看,確定一個不規則圖形的面積當然不是一件易事,但如果這個不規則圖形能夠用一個等面積的正方形替換,那麼,確定原不規則圖形面積的問題就變成了確定正方形面積的簡單問題。
對於希臘數學家來說,探討面積的求法是一個特別具有吸引力的課題,為此,他們作出了許多巧妙的幾何圖形。
解數學問題,答案常常是一步一步推導出來的,求面積也是如此。第一步先要求出一個大體上“規則”的圖形的面積,然後再以此為基礎,繼續推導出更不規則、更稀奇古怪的圖形的面積。
希波克拉底時代的希臘人利用上述方法可以將雜亂無章的不規則多邊形變為等面積的正方形。但是,這一成就卻因一個明顯的事實而減色不少,即這些圖形都是直線圖形一它們的邊 雖然數量眾多,並構成各種奇形怪狀的角度,但都只是直線。更嚴重的挑戰是,曲邊圖形(即所謂曲線圖形)是否也可以用等價平方表示。起初,人們認為,這似乎是根本不可能的,因為顯然沒有辦法用圓規和直尺將曲線拉直。因此,當希波克拉底於公元前5世紀成功地將一種稱為“新月形”的曲線圖形化為正方形時,世人驚得目瞪口呆。
球面二角形亦稱月形或瓜瓣形,是一種特殊的球面圖形,球面上兩個對徑點和以這兩點為端點的兩個半大圓所圍成的球面圖形稱為球面二角形。構成球面二角形的兩個半大圓稱為它的邊,兩個對徑點稱為它的頂點,一個頂點和兩條邊所構成的球面角稱為它的角,球面二角形也可以看做是半圓周繞直徑旋轉某一角度α所成的旋轉面,球面二角形的大小可以用其角的大小來表徵,其角是銳角的球面二角形稱為銳球面二角形;其角是直角的球面二角形稱為直球面二角形;其角是鈍角的球面二角形稱為鈍球面二角形;其角是優角(大於180°,小於360°)的球面二角形稱為優球面二角形。
球面月形的面積
介於相交的兩個半大圓之間的球面部分,稱為球面月形,換言之,即球面被以一直徑為棱的二面角所截的部分。
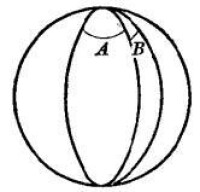
圖5
定理 同球兩月形之比等於它們的角之比。
且有以下結論:
1° 角相等的兩個月形是全等的,因為迭合了它們相應的二面角,它們便迭合了。
2° 以兩月形A,B的角之和為角的月形C,其面積為A,B面積之和,只要使兩月形成為相鄰的(兩個相鄰的二面角所確定的月形,稱為相鄰的),就顯然了(圖5),而由1°,我們是可以這樣辦的。
從上面所指出的兩點,可以推出我們想要證明的命題。
系 月形的面積是它的角的兩倍(在所設的單位制下)。
因為角為直角的月形顯然是球面的四分之一,因此它的面積是數π,至於它的角則為π/2。
由於這個月形面積的度量與角的度量之比等於2,所以對於一切其他月形也如此(上述定理) 。
