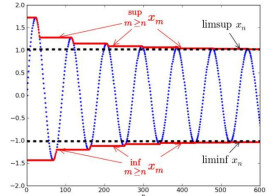
上確界

上確界是序理論中最基礎的概念之一。

給定偏序集，A是S的子集，則A的上確界（亦稱最小上界）supA定義為滿足以下條件的元素：

Ⅰ.

Ⅱ.

Ⅲ.，若a滿足，則。

即：supA是A的所有上界組成的集合的最小元（若存在）。

A的上確界亦被記為sup(A)，lubA，LubA或∨A。

上確界在序理論中的對偶概念是下確界。

並非所有的A都能找到上確界。

具體到數學分析中。一個實數集合A，若有一個實數M，使得A中任何數都不超過M，那麼就稱M是A的一個上界。在所有那些上界中如果有一個最小的上界，就稱為A的上確界。即設有一實數集，實數集A的上確界supA被定義為如下的數：

（1） （即supA是A的上界）

（2），（即再小一點就不是上界）

一個數集若有上界，則它有無數個上界；但是上確界卻只有一個，這可以直觀地從上確界（最小上界）的含義中看出來。並且如果一個數集若有上界，則它一定有上確界。

在一般的數學分析學教材中，實數理論一章，為了說明實數的緊性，有一系列的定理，理論比較嚴密的前蘇聯教材一般是以戴德金分割定理為出發點證明其它的等價定理。而我國教材為了簡化，很多都是從確界定理為出發點進行的證明，其他說明實數的連續性的定理還有區間套定理，有限復蓋定理等等。

確界定理是實數理論中最基本的結論之一，是實數集緊性的體現。

定理：任何有上界(下界）的非空實數集必存在上確界（下確界）。

用戴德金分割定理證明。

戴德金分割定理：對實數集R的任意一個滿足不空、不漏、不亂的劃分A和B，都存在唯一的一個分點

滿足,，.

記給定非空集合為X。取定B為X的所有上界的集合，。下證A、B為劃分。

不空：由於X非空，可取，易知不可能為X的上界，故A非空。B非空給定；

不漏：由 知；

不亂：設 ，則由知不是X的上界，即，，但又由是X的上界知，綜上， 又，矛盾。不亂得證。

故存在唯一的一個分點滿足，，。下證分點為上確界，即 。

若不然， ，則 ，但此時就有，由知 ，與是劃分A和B的分點相矛盾。故

。

下確界同理。證畢。