分佈參數系統
分佈參數系統
分佈參數系統,狀態變化不能只用有限個參數而必須用場(一維或多維空間變數的函數)來描述的系統。在實際問題中,參數的分佈性質是普遍存在的。在很多情況下可以部分甚至全部地忽略這種分佈性質,以便簡化對問題的研究。
狀態變化不能只用有限個參數而必須用場(一維或多維空間變數的函數)來描述的系統。在實際問題中,參數的分佈性質是普遍存在的。在很多情況下可以部分甚至全部地忽略這種分佈性質,以便簡化對問題的研究。例如,對於一個有質量分佈的彈性飛行器,在研究它的扭轉運動時,必須考察其內部各點的運動,把它當作分佈參數系統。但在研究它的運動軌線時,就不必逐點考慮其內部運動,而把質量集中到質心來分析,即把它當作集中參數系統。可以用有限個變數描述的系統,稱為集中參數系統或集總參數系統。分佈參數系統的典型實例有:電磁場、引力場、溫度場等物理場,彈性梁型的運動體,大型加熱爐,水輪機和汽輪機,化學反應器中的物質分佈狀態,長導線中的電壓和電流等控制對象,環境系統(如污染物在一區域內的分佈),生態系統(如物種的空間分佈),社會系統(如人口密度分佈)等。此外,若運動過程包含因在某種場內傳遞而造成的時滯,則這種時滯系統也屬於分佈參數系統。分佈參數系統廣泛應用於熱工、化工、導彈、航天、航空、核裂、聚變等工程系統,以及生態系統、環境系統、社會系統等。
1954年錢學森在《工程式控制制論》一書中討論了熱傳導過程的分佈參數系統問題,最早使用了無窮階傳遞函數的概念。1961年А.Г.布特科夫斯基以熱軌鋼問題為背景,討論了分佈參數系統的最優控制問題。1964年王耿介研究了分佈參數系統的穩定性、能控性、能觀測性、最優控制等問題。在這之前,J.L.萊恩斯在現代泛函分析和偏微分方程理論的基礎上,對分佈參數系統理論進行過廣泛深入的研究。隨後宋健、關肇直等人對分佈參數受控對象和集中參數控制器互相耦合的分佈參數控制系統從理論上進行了系統的研究。在分佈參數系統理論的發展過程中,頻率域方法與時間域方法是并行發展的。從20世紀60年代開始它們有了很大發展。現代偏微分方程和泛函分析理論成果的應用,為分佈參數系統建立了嚴格的理論基礎,提供了有力的研究工具。在分佈參數系統的鎮定、最優控制、能控性和能觀測性以及分佈參數的辨識和濾波問題上,都已取得類似於集中參數系統的成果,也可認為是集中參數系統相應結果的推廣。但在這個領域中可用來解決工程實際問題的成果還不多。
受控對象或控制器需要用分佈參數描述的控制系統稱為分佈參數控制系統。在工程技術中除受控對象外,控制裝置或執行機構也可能是分佈參數系統。例如當液壓或氣動執行機構的油路或氣路結構複雜且線路過長時,在其運動規律中必須同時考慮流體(工作體)本身的狀態變化,這種變化狀態也是由分佈參數描述的。但這種情況常常不是所希望的。分佈參數控制器由於難以實現而很少採用。大量的情況為受控對象是分佈參數系統,而控制器是集中參數系統。分佈參數控制系統有三種控制方式。①點控制方式:將控制作用加在控制對象的幾個孤立點處。②分佈控制方式:將控制作用加在控制對象的幾個區域內。③邊界控制方式:將控制作用加在控制對象邊界上。這種控制又有點控制和分佈控制之分。類似地,測量方式也可分為點測量、分佈測量和邊界測量。
分佈參數系統
分佈參數系統
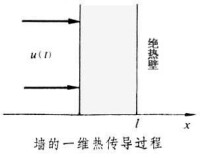
應用拉普拉斯變換可求得傳遞函數
式中ch(·)為雙曲餘弦函數。傳遞函數是超越函數且同時依賴於空間變數x和複數復量s,具有無窮多個極點,稱為無窮階傳遞函數。
在分佈參數控制系統中引進反饋作用的問題也比在集中參數系統中複雜得多。由於大多數情況下控制器和檢測裝置都採用集中參數類型,對於分佈參數系統不易實現完整的狀態反饋或輸出反饋,系統的能控性和能觀測性都比較弱。分佈參數控制系統的綜合設計問題的不確定性很大,也複雜得多。
錢學森、宋健:《工程式控制制論》(修訂版),科學出版社,北京,1980。
J.L.Lions, Optimal Control of Systems Governed by Partial Differential Equations, Springer-Verlag, Berlin,1971.