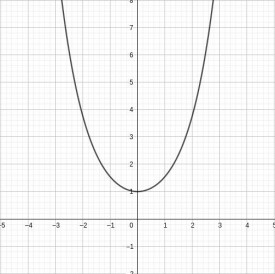
雙曲餘弦函數
雙曲餘弦函數
雙曲餘弦函數是雙曲函數的一種。我們知道三角函數分正弦sin、餘弦cos、正切tan、餘切cot、正割sec、餘割csc六種。那麼，類似的，雙曲函數也分為雙曲正弦、雙曲餘弦、雙曲正切、雙曲餘切、雙曲正割、雙曲餘割六種。雙曲餘弦函數也是其中一種。雙曲餘弦函數記作cosh，也可簡寫為ch。
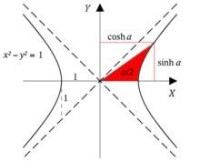
雙曲函數的定義示意圖
而其中，就是的雙曲餘弦函數。
最後，經由複雜的計算推得。。
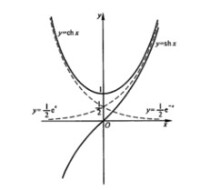
雙曲餘弦函數和雙曲正弦函數的圖像
雙曲餘弦函數在定義域內是偶函數。可以證明：
取的負值。又得：
根據加法交換律，可得出 。根據偶函數的定義，可知該函數是偶函數。它關於軸對稱。
雙曲餘弦函數，在區間內它是單調減少的，在區間內它是單調增加的。是該函數的最小值
可以用導數證明。由於分母是永遠大於0的，而分子中也是永遠大於0。只有在時是等於0。在時。。在時。。得出當時，雙曲餘弦函數的導數永遠小於0。當時，雙曲餘弦函數的導數永遠大於0。那麼它在內單調遞減的，在內單調遞增。在時，最小值為1。無最大值。
無論是雙曲餘弦函數，還是雙曲正弦函數、雙曲正切函數，它們都不是周期函數。
由於那麼雙曲餘弦函數的二階導數為
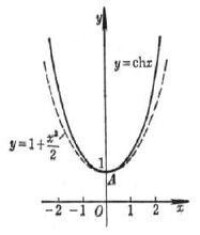
雙曲餘弦函數圖像
而根據函數凹凸性的判定方法（定理）：
設在上連續，在內具有一階導數和二階導數，那麼：
（1）若在內，，則在上的圖形是凹的。
（2）若在內，，則在上的圖形是凸的。
根據上面的函數凹凸性判斷定理。得出那麼無論是在那個單調區間，雙曲餘弦函數都是凹函數。
懸鏈線
均勻引力作用下下垂相似。這條曲線稱作懸鏈線。懸鏈線就是雙曲餘弦函數的圖像。
懸鏈線的數學表達式為其中，a為常數。當時，所得的函數（圖像）正好是雙曲餘弦函數（圖像）。
雙曲餘弦和雙曲正弦的二倍角公式。
雙曲餘弦以及雙曲正弦的半形公式有：
等式1：
等式1的證明：等式2：（雙曲正切的定義式，與三角函數中的正切類似）
等式3：（雙曲函數和指數函數的關係）
等式4：（雙曲函數和指數函數的關係）
雙曲餘弦函數的導數是雙曲正弦函數。即
也可以轉化為
其中，C為常數。可見，雙曲餘弦函數的不定積分，除去常數C，也是雙曲正弦函數。
另有公式(這裡，大寫的C為常數）
另外，關於雙曲餘弦函數還有如下的公式：
(其中，C為任意常數）
雙曲餘弦函數的泰勒展開式為：
即：
雙曲餘弦函數的反函數是反雙曲餘弦函數。它記作。根據反函數的定義，它的定義原本應該是：
其中，滿足條件：。
反雙曲餘弦函數的圖像原本有軸上方的一支和軸下方的一支。即且這兩支關於軸對稱。但是，這樣子會造成一個自變數對應兩個函數值，不符合函數的定義。
為了符合函數的定義，一般取x軸上方的那一支。因而得到了反雙曲餘弦函數的定義式。
雙曲餘弦的反函數，即反雙曲餘弦函數的定義域為,它在區間上是單調增加的。
基本信息
- 中文名
- 雙曲餘弦函數
- 外文名
- Hyperbolic cosine function
- 應用學科
- 數學
- 符號
- cosh（或ch）