絕對定向
絕對定向
絕對定向是航空攝影測量用語,根據像控點確定立體模型比例尺和在地面坐標系中所處方位的過程。
將已相對定向好的模型進行旋轉和平移,使它與地面量測的數據相匹配,從而在模型中建立起地面坐標系統。將浮動測標切准模型能辨認的所有控制點,就能完成這項工作。控制點的地面坐標是巳知的,並已貯存在計算機中。模型坐標是自動記錄的。計算機按最小二乘法利用這些存貯的數據(假定這些數據是滿足要求的)進行計算,確定了每個攝影站的新的常數。余差能說明解的可靠性。假如需要的話,也可以將相對定向和絕對定向合成一個操作步驟。
利用視差分佈情形所提供的線索,通過對兩個投影器的調整,就可以建立地面的三維模型。然而這個模型的比例尺是未知的,且對儀器基準平面來說是傾斜的。因此模型的絕對定向包括確定模型的比例尺以及模型置平。這兩項操作應按照規定的次序實施,為此還必須要有某些輔助資料。
確定模型比例尺
為了確定模型此例尺,最低限度必須知道模型上一個線段的實地長度。要做到這一點,只要在地面上測量一條直線,而這條直線兩個端點在模型表面上也要能識別出來。但是更常有的情形是已經知道了這兩個端點的坐標。由這些數據可以得出:
(1)模型的此例尺係數,
(2)所測繪模型的定向,
(3)所測繪模型在參考坐標系內的位置。
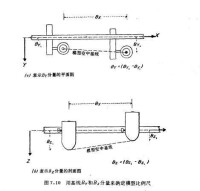
利用基線確定比例尺圖示
模型的置平
要將模型置平,必須在兩個方向上使模型表面的坡度與地面相同。為了達到最大的靈敏度,這兩個方嚮應彼此正交。除了水平的水面可作參考外,一般難以判定模型傾斜程度,因此又必須利用已識別的模型點的坐標。最低限度的獨立高程點分佈,但是這些獨立高程點可以將模型置平。然而,如果只有三個點,就不能對定向進行檢查,因此實際上最少要有四個高程點。對於主要因模型傾斜而造成的方向的任何傾斜誤差,以及因模型傾斜誤差而引起的其他方向的任何誤差,利用高程式控制制點能非常容易地將模型置平。當高程式控制制點依照一定順序分佈時,只要重複幾次,就能很快使模型處於正確位置。如果所用的高程式控制制點超過四個,理論表明,第五點的最佳位置,應在基線中點垂線的某一點上。當第五點處於此位置時,因相對定向剩餘誤差而產生的模型表面上圓柱體彎曲的任何傾向,都可以被發現。
根據絕對定向元素分析可知,絕對定向要求有兩個平高控制點和不在兩點連線上的另一高程點,實際作業時為了檢查高程置平和平面對點精度,進行誤差配賦以提高定向精度,一般要求布設4個平高控制點,根據四點確定模型比例尺和方位(兩點的距離愈遠精度愈高),用四點置平航向高程。
假定一條航線的第一個模型已完成了絕對定向,我們希望不用其他外部控制數據而把這一定向擴展到下一個模型。
第二個模型可以由2、3兩張像片進行相對定向來構成。由於像片航向重疊不少於55%,在兩個模型M和M之間得到一個有用的重疊部分。因此這兩個模型表面的重疊部分的信息數據可以用於第二個模型的絕對定向。很清楚,有足夠的數據可用來確定模型此例尺和在Ω方向上的模型定向。但是這些重疊部分的數據對於擴展Φ方向的定向仍嫌不足,如果要想進行這種擴展,將是一種不可靠的外推法。
因此要完成這一定向,我們看到另外一個因素,就是兩個模型具有公共像片2。在第一個模型絕對定向之後,這張公共像片2的方位被認為是已知的。因此在第二個模型相對定向後,將此模型旋轉直到公共像片2的方位正確為止,並改變比例尺直到底點距離正確為止,這樣就完成了絕對定向。我們知道這兩個因素所提供的信息數據對於擴展第一個模型的定向來說是足夠的。實際上沒有校驗的只有一個Φ定向元素。所有的空中三角測量方法,不管是模擬法還是解析法,總是應用了上述的概念。
